2025-09-11

メモ: 二種類のベルヌーイ数について(続き): オイラー・マクローリンの和公式

数学整数論

オイラー・マクローリンの和公式
和公式の導出
和公式の導出(続き)
演算子を用いた導出
ゼータ関数の特殊値 ζ(1-m) とベルヌーイ数

1. オイラー・マクローリンの和公式

ベルヌーイ数が出てくる公式にオイラー・マクローリンの和公式がある。
オイラー・マクローリンの和公式は、積分の台形近似 $\int_k^{k+1}f(x)dx \approx \frac{1}{2}f(k) + \frac{1}{2}f(k+1)$ を、逆に和を積分で近似していると考えて、さらに和を取って、

$\displaystyle \sum_{k=a}^b f(k) = \frac{1}{2}f(a) + \sum_{k=a}^{b-1}(\frac12 f(k) + \frac12 f(k+1)) + \frac12 f(b) \\ \displaystyle \qquad \qquad \approx \frac{1}{2}f(a) + \int_a^b f(x)dx + \frac{1}{2}f(b)$

と近似して、誤差の評価式にベルヌーイ数とベルヌーイ多項式を使ったものだと考えることができる。
ただ、上の式のようにaからbまでの和を考えた場合のオイラー・マクローリンの和公式は、r=2以上のベルヌーイ数しか出てこないので、 B⁺ と B^- の違いは影響しない。(和公式の導出過程でも、B⁺_r を使っているとも B^-_r を使っているとも、どちらと考えることもできる)。
和を取る時に端の項を除いて $\displaystyle \sum_{a \leq k < b} f(k)$ や $\displaystyle \sum_{a < k \leq b} f(k)$ を考えた場合、

$\begin{eqnarray} \sum_{k=a}^{b-1} f(k) & \approx & \frac{1}{2}f(a) + \int_a^b f(x)dx - \frac{1}{2}(b) \\ \sum_{k=a+1}^{b} f(k) & \approx & - \frac{1}{2}f(a) + \int_a^b f(x)dx + \frac{1}{2}(b) \end{eqnarray}$

となるけど、 $B^{-}_1 = -\frac12, B^{+}_1 = \frac12$ なので、

$\begin{eqnarray} \sum_{k=a}^{b-1} f(k) & \approx & \left[B^{-}_1 f(x) \right]_a^b + \int_a^b f(x)dx \\ \sum_{k=a+1}^{b} f(k) & \approx & \left[B^{+}_1 f(x) \right]_a^b + \int_a^b f(x)dx \end{eqnarray}$

と書くことができ、ベルヌーイ数B₁ も使った形の公式が得られる。

2. 和公式の導出

オイラー・マクローリンの和公式を導くために、 $\int_0^1 f(x) dx$ の台形近似

$\displaystyle \int_{0}^{1} f(x) dx \approx \frac{1}{2}f(0) + \frac{1}{2}f(1)$

に注目する。ここで、1次のベルヌーイ多項式 $B_1(x) = x - \frac12$ を使うと、右辺は

$\displaystyle \frac{1}{2}f(0) + \frac{1}{2}f(1) = -B_1(0) f(0) + B_1(1) f(1) = \left[B_1(x) f(x)\right]_0^1$

と書き直すことができる。このことに注目すると $\int_0^1 f(x) dx$ は部分積分により

$\displaystyle \int_{0}^{1} f(x) dx = \left[B_1(x) f(x)\right]_0^1 - \int_0^1 B_1(x)f'(x) dx$

と変形できる。これは「台形近似 + 誤差項」と考えることができる。
次に誤差項にあたる $\int_0^1 B_1(x)f'(x) dx$ をさらに部分積分で変形することを考える。この時、g'(x) = B₁(x) かつ、g(0) = g(1) となる関数 g(x) を使って、

$\displaystyle \int_0^1 B_1(x)f'(x) dx = \left[ g(x) f'(x) \right]_0^1 - \int_0^1 g(x)f''(x) dx$

と部分積分する。なぜかというと、 $\int_1^2 f(x) dx, \int_2^3 f(x) dx, \cdots$ などについても同様の変形をしたときに $g(1)(f'(1) - f'(0)), g(1)(f'(2) - f'(1)), g(1)(f'(3) - f'(2)), \cdots$ が現れ、和を取ったときに端以外の項が打ち消し合って都合が良いので。
さてこの g(x) というは 2次のベルヌーイ多項式を2で割った $\frac{B_2(x)}{2}$ にほかならない。(ベルヌーイ多項式は k≠1 のとき B_k(0) = B_k(1) となる。また、B_k'(x) = k B_k-1(x) となるのはべき乗和多項式の微分の関係式から分かる)。したがって、

$\displaystyle \int_{0}^{1} f(x) dx = \left[\frac{B_1(x)}{1} f(x)\right]_0^1 - \left[ \frac{B_2(x)}{2} f'(x) \right]_0^1 + \frac{1}{2}\int_0^1 B_2(x) f''(x) dx$

と変形される。さらに同様の部分積分をする。 $\left(\frac{B_3(x)}{3}\right)' = B_2(x)$ で B₃(0) = B₃(1) なので、

$\displaystyle \int_{0}^{1} f(x) dx = \left[B_1(x) f(x)\right]_0^1 - \frac{1}{2!}\left[ B_2(x) f'(x) \right]_0^1 + \frac{1}{3!}\left[ B_3(x) f''(x) \right]_0^1 - \frac{1}{3!}\int_0^1 B_3(x) f^{(3)}(x) dx$

が得られる。以下、同様の部分積分を繰り返していくと、

$\displaystyle \int_{0}^{1} f(x) dx = \sum_{l=1}^{M} \frac{(-1)^{l-1}}{l!} \left[ B_l(x) f^{(l-1)}(x) \right]_0^1 + \frac{(-1)^{M}}{M!} \int_0^1 B_M(x) f^{(M)}(x) dx$

となる。より一般的にした $\int_{k}^{k+1} f(x) dx$ に対しては、B_l(x) の代わりに B_l(x - k) = B_l(x - ⌊x⌋) を使って同様の変形をして、

$\displaystyle \int_{k}^{k+1} f(x) dx = \sum_{l=1}^{M} \frac{(-1)^{l-1}}{l!} \left[ B_l(x-\lfloor x \rfloor ) f^{(l-1)}(x) \right]_k^{k+1} + \frac{(-1)^{M}}{M!} \int_k^{k+1} B_M(x - \lfloor x \rfloor) f^{(M)}(x) dx$

を得る。この式を見ると l=1 の項も l≧2 の項も同じ形でまとまっているけど、ここからの変形で1次の項だけ別扱いされる。
l≧2 の項は、和を取ったに打ち消し合うこと念頭に作られている。実際、l≧2 の時の

$\left[ B_l(x-\lfloor x \rfloor) f^{(l-1)}(x) \right]_{k}^{k+1} = B_l (f(k+1) - f(k))$

となっていて、これらは和を取ったときに端の値以外は打ち消し合う。
一方、l=1の項は $\displaystyle \frac{1}{2}f(0) + \frac{1}{2}(1)$ や $\displaystyle \frac{1}{2}f(k) + \frac{1}{2}(k+1)$ で、これらは合わさって和 $\sum f(x)$ (＋端でのズレ) になる。

3. 和公式の導出(続き)

和公式を導くために先程の式

$\displaystyle \int_{0}^{1} f(x) dx = \sum_{l=1}^{M} \frac{(-1)^{l-1}}{l!} \left[ B_l(x) f^{(l-1)}(x) \right]_0^1 + \frac{(-1)^{M}}{M!} \int_0^1 B_M(x) f^{(M)}(x) dx$

をさらに変形する。まず l≧2 の部分。 B_l(0) = B_l(1) = B_l や、ベルヌーイ数は l≠1の時 B_l = (-1)^l B_l を満たすという性質を使うと、

$\displaystyle \sum_{l=2}^{M} \frac{(-1)^{l-1}}{l!} \left[ B_l(x) f^{(l-1)}(x) \right]_0^1 = \sum_{l=1}^{M} \frac{- B_l}{l!} \left[ f^{(l-1)}(x) \right]_0^1$

となる。
l=1の項は、
$\begin{eqnarray} \left[ B_1(x) f(x) \right]_0^1 & & & = & \frac{1}{2} f(0) + \frac{1}{2} f(1) \quad && \text{(そのまま展開)} \\ &=& f(1) - ( \frac{1}{2} f(1) - \frac{1}{2}f(0) ) &=& f(1) - B^+_1 \left[ f(x) \right]_0^1 \quad && \text{(打ち消し合う形1)}\\ &=& f(0) - ( -\frac{1}{2} f(1) - (-\frac{1}{2})f(0) ) &=& f(0) - B^-_1 \left[ f(x) \right]_0^1 \quad && \text{(打ち消し合う形2)}\end{eqnarray}$

と変形できる。「そのまま展開」の形だと1次のベルヌーイ数 B⁺₁ も B^-₁ も出てこない。「打ち消し合う形」にすると l≧2 の時と同じ形の項が出てくるので式をまとめられる。(ここまでの式変形は積分範囲をkからk+1で考えた場合もほぼ同様にできる)。
あとは積分範囲を整数aからbまでつなげて左右の項を適宜入れ替えれば、和の範囲がそれぞれ違う3種類のオイラー・マクローリンの和公式

$\begin{eqnarray} \sum_{k=a}^{b} f(k) &=& \int_a^b f(x) dx + \frac{1}{2}(f(a) + f(b)) + \sum_{l=2}^{M} \frac{B_l}{l!} \left[ f^{(l-1)}(x) \right]_a^b + \frac{(-1)^{M-1}}{M!} \int_a^b B_m(x - \lfloor x \rfloor) f^{(M)}(x) dx \\ \sum_{k=a+1}^{b} f(k) &=& \int_a^b f(x) dx + \sum_{l=1}^{M} \frac{B^{+}_l}{l!} \left[ f^{(l-1)}(x) \right]_a^b + \frac{(-1)^{M-1}}{M!} \int_a^b B_m(x - \lfloor x \rfloor) f^{(M)}(x) dx \\ \sum_{k=a}^{b-1} f(k) &=& \int_a^b f(x) dx + \sum_{l=1}^{M} \frac{B^{-}_l}{l!} \left[ f^{(l-1)}(x) \right]_a^b + \frac{(-1)^{M-1}}{M!} \int_a^b B_m(x- \lfloor x \rfloor) f^{(M)}(x) dx\end{eqnarray}$

が得られる。
B⁺₁ のベルヌーイ数を使う和公式では始端の項 f(a) が和に含まれず、B^-₁ のベルヌーイ数を使う和公式では終端の項 f(b) が和に含まれない。
特に f(x) = x^r として、a=0、b=n で和公式を適用するとべき乗和多項式が得られる。0〜n の始端を含めない和は $\sum_{k=1}^{n} k^r$ なのでベルヌーイ数 B⁺₁ を使う和公式により S⁺_r(n) が得られ、終端を含めない和は $\sum_{k=0}^{n-1} k^r$ なのでベルヌーイ数 B^-₁ を使う和公式から S^-_r(n) が得られる。

4. 演算子を用いた導出

オイラー・マクローリンの和公式を上でおこなったような仕方で導いた場合、1次の項だけ式変形の流れが異なることもあり、ベルヌーイ数 B⁺₁ にしてもベルヌーイ数 B^-₁ にしても、いくらか人工的に公式に付け加えたようにも見える。
しかし演算子を使って形式的にオイラー・マクローリンの和公式を導くとまた違って見える。(クヌース他『コンピュータの数学』9.5節、ヴェイユ『数論: 歴史からのアプローチ』3章XVII節など)
まず差分演算子(前進差分演算子) Δ を考える。差分演算子 Δ は、関数 f(x) に適用したときに

(Δf)(x) = f(x+1) - f(x)

という新たな関数が得られるという演算子。
次に差分演算子の逆演算子にあたる和分演算子 Σ を考える。
これは関数 f(x) に適用すると (ΔF)(x) = f(x) となる「差分の原始関数」F(x) を与える演算子だけど、周期1の関数 C(x) は差分を取ると (ΔC)(x) = C(x+1) - C(x) = 0 なので、差分の原始関数 F(x) に対して F(x) + C(x) も差分の原始関数となり、差分の原始関数はひとつには決まらない。(これは微分の原始関数(普通の原始関数)が積分定数Cを使って F(x) + C と表されることと類似している)。xが整数のときを考えると、

$\displaystyle (\Sigma f)(x) = \sum_{k=c}^{x-1} f(k) + C$

と表すことができる。(cは整数の定数、Cは定数)。前進差分 (Δf)(x) = f(x+1) - f(x) の逆演算Σを考えた時、和の末項はxではなく x-1 になる。

さらに差分演算子Δと微分演算子Dを結びつける。
f(x+1) はテーラー展開により

$\displaystyle f(x+1) = \sum_{k=0}^{\infty} \frac{f^{(k)}(x)}{k!} = \sum_{k=0}^{\infty} \frac{(D^k f)(x)}{k!} = \left(\left(\sum_{k=0}^{\infty} \frac{D^k }{k!}\right) f \right)(x)$

と書けるけど、演算子の部分 $\sum_{k=0}^{\infty} \frac{D^k }{k!}$ は指数関数のテーラー展開と同じ形をしているので e^D と書くことにする。e^Dは f(x) を f(x+1) に変換するシフト演算子を表す。すると

$\displaystyle (\Delta f)(x) = f(x+1) - f(x) = (e^D f)(x) - f(x) = ( (e^D - I)f)(x)$

となる(ここで I は (If) = f となる恒等演算子)。つまり演算子Δは「Δ = e^D - I」と書ける。

和分演算子 Σ は差分演算子 Δ の逆演算子だったので $\Sigma = \Delta^{-1} = \frac{1}{\Delta}$ と分数の形で書いてみると、「Δ = e^D - I」となることと合わせて

$\displaystyle \Sigma = \frac{1}{\Delta} = \frac{1}{e^D - I} = \frac{1}{D}\frac{D}{e^D - I}$

と書き換える。するとベルヌーイ数 B^- の母関数

$\displaystyle \frac{z}{e^z - 1} = \sum_{k=0}^{\infty} \frac{B^{-}_k}{k!} z^k$

と同じ形が現れたので、

$\displaystyle \frac{D}{e^D - 1} = \sum_{k=0}^{\infty} \frac{B^{-}_k}{k!} D^k$

として変形を続けると

$\displaystyle \Sigma = \frac{1}{D} \sum_{k=0}^{\infty} \frac{B^{-}_k}{k!} D^k = \frac{1}{D} + \sum_{k=1}^{\infty} \frac{B^{-}_k}{k!} D^{k-1} \\ \displaystyle \qquad = \int + \sum_{k=1}^{\infty} \frac{B^{-}_k}{k!} D^{k-1}$

となる。1/Δ が差分演算子 Δ の逆演算子 Σ だったように、 1/D は微分演算子 D の逆演算子 ∫ とみなした。
よって、和分演算子 Σ を f に適用して x を整数の時を考えると

$\displaystyle (\Sigma f)(x) = \sum_{k=c}^{x-1} f(k) = \int_d^x f(t) dt + \sum_{l=1}^{\infty} \frac{B^{-}_l}{l!} f^{(l-1)}(x)$

となってオイラー・マクローリンの和公式とだいたい同じ式(ただし剰余項がなく発散のことも何も考えていない式)が得られる。
さらに (Σf)(b) - (Σf)(a) を考えると

$\displaystyle (\Sigma f)(b) - (\Sigma f)(a) = \sum_{k=a}^{b-1} f(k) = \int_a^b f(t) dt + \sum_{l=1}^{\infty} \frac{B^{-}_l}{l!} \left[f^{(l-1)}(x)\right]_a^b$

となり、よりオイラー・マクローリンの和公式に近い式が得られる。
また ∫ = D^-1 だったので f(x) の原始関数を f^(-1) と書くことにすると、 $\int_a^b f(t)dt = \frac{B_0}{0!} \left[ f^{(-1)}(x) \right]_a^b$ と書け、

$\displaystyle \sum_{k=a}^{b-1} f(k) = \sum_{l=0}^{\infty} \frac{B^{-}_l}{l!} \left[f^{(l-1)}(x)\right]_a^b$

のようにさらにまとめた形で書ける。

ここまで差分演算子 Δ を
前進差分 (Δf)(x) = f(x+1) - f(x)
を表すものとして使ってきたけど、
後退差分 (Δf)(x) = f(x) - f(x-1)
だと考えると、(f(x-1)のテーラー展開から、f(x)をf(x-1)に変換する演算子が e^-Dと書けることが分かるので) 後退差分演算子を Δ = I - e^-D と書ける。
その逆演算子 Σ は x が整数の時 $\displaystyle (\Sigma f)(x) = \sum_{k=c}^{x} f(k)$ となる演算子(和を取る末項が x-1 ではなく x になる)になり、

$\displaystyle \Sigma = \frac{1}{\Delta} = \frac{1}{I - e^{-D}} = \frac{1}{D}\frac{D}{I - e^{-D}}$

となる。
あるいは
「後退差分 (f(x)-f(x-1))」=「前進差分 (f(x+1)-f(x))」×「e^-D ((x)を(x-1)にシフト)」
なので
「後退差分の逆演算子」=「前進差分の逆演算子 $\frac{1}{e^D - I}$ 」×「e^D ((x)を(x+1)にシフト)」
として、

$\displaystyle \Sigma = \frac{e^D}{e^D - I} = \frac{1}{D}\frac{D e^D}{e^D - I}$

となる。いずれにしても、ベルヌーイ数 B⁺ の母関数

$\displaystyle \frac{z}{1-e^{-z}} = \frac{z e^z}{e^z-1} = \sum_{k=0}^{\infty} \frac{B^{+}_k}{k!} z^k$

と同じ形の部分式が現れるので、前と同様の式変形を行っていき最後に (Σf)(b) - (Σf)(a) を考えると、前と同様の式(使っているベルヌーイ数と和の範囲だけ異なる式)

$\displaystyle \sum_{k=a+1}^{b} f(k) = \int_a^b f(t) dt + \sum_{l=1}^{\infty} \frac{B^{+}_l}{l!} \left[f^{(l-1)}(x)\right]_a^b = \sum_{l=0}^{\infty} \frac{B^{+}_l}{l!} \left[f^{(l-1)}(x)\right]_a^b$

が得られる。

4. ゼータ関数の特殊値 ζ(1-m) とベルヌーイ数

正整数 m を取ると、ゼータ関数の 1-m の時の値は

$\displaystyle \zeta(1-m) = -\frac{B^{+}_m}{m} = (-1)^{m+1}\frac{B^{-}_m}{m}$

となることが知られている。このことをオイラー・マクローリンの和公式を使って導いてみる。

まずゼータ関数は

$\displaystyle \zeta(s) = \sum_{k=1}^{\infty} \frac{1}{k^s}$

と定義される。この無限級数は $\Re(s) > 1$ の時しか収束しないけど、オイラー・マクローリンの和公式を使って導かれる式はこれより広い領域で収束する。

この無限級数から有限範囲を取り出してオイラー・マクローリンの和公式を適用する。ここでは、ベルヌーイ数 B⁺ を使う方の公式

$\displaystyle \sum_{k=a+1}^{b} f(k) = \frac{B^{+}_0}{0!} \int_a^b f(x) dx + \sum_{l=1}^{M} \frac{B^{+}_l}{l!} \left[ f^{(l-1)}(x) \right]_a^b + R_M$

を使う。(後ろの項と形を合わせるために右辺初項に $\frac{B^+_0}{0!}=1$ をつけた。また剰余項の部分は R_M と省略した)。この式で f(k) = k^-s として、その微分は下降階乗を使って

$\displaystyle f^{(l-1)}(x) = (-s)(-s-1)(-s-2)\ldots(-s-l+1)x^{-s-l+1} = (-s)^{\underline{l-1}}x^{-s-l+1}$

と書くことにして、和公式の範囲を a=0、b=N としたものを使うと次のようになる。

$\begin{eqnarray} \sum_{k=1}^{N} \frac{1}{k^s} &=& \frac{1}{1^s} + \sum_{k=1+1}^{N} k^{-s}\\ &=& \frac{1}{1^s} + \frac{B^{+}_0}{0!} \int_1^N x^{-s} dx + \sum_{l=1}^{M} \frac{B^{+}_l}{l!} \left[ (-s)^{\underline{l-1}} x^{-s-l+1} \right]_1^N + R_M(N,s) \\ &=& \frac{1}{1^s} + \frac{B^{+}_0}{0!} \left[\frac{1}{-s+1}x^{-s+1}\right]_1^N + \sum_{l=1}^{M} \frac{B^{+}_l}{l!} \left[ \frac{(-s+1)^{\underline{l}}}{-s+1} x^{-s-l+1} \right]_1^N + R_M(N,s) \\ &=& \frac{1}{1^s} + \sum_{l=0}^{M} \frac{B^{+}_l}{l!} \left[ \frac{(-s+1)^{\underline{l}}}{-s+1} x^{-s-l+1} \right]_1^N + R_M(N,s) \\ &=& \frac{1}{1^s} + \frac{1}{-s+1}\sum_{l=0}^{M} \frac{(-s+1)^{\underline{l}}}{l!}B^{+}_l \left[ x^{-s-l+1} \right]_1^N + R_M(N,s) \end{eqnarray}$

ここで、 $\Re(s) > 1$ とした上で、 $N \to \infty$ とすると、剰余項 R_M(N,s)も収束し

$\displaystyle \zeta(s) = \sum_{k=1}^{\infty} \frac{1}{k^s} = \frac{1}{1^s} - \frac{1}{-s+1}\sum_{l=0}^{M} \frac{(-s+1)^{\underline{l}}}{l!}B^{+}_l + R_M(s)$

となる。
無限級数 $\sum_{k=1}^{\infty} \frac{1}{k^s}$ は $\Re(s) > 1$ で収束するけど、導いた右辺の式は剰余項 R_M(s) が $\Re(s) > 1 - M$ で収束し、より広い範囲のゼータ関数の値を定めている。この式を使って ζ(1-m) の値を求めると l>m の項が( $m^{\underline{l}}=0$ なので)消えて、

$\begin{eqnarray} \zeta(1-m) &=& \frac{1}{1^s} - \frac{1}{m}\sum_{l=0}^{m} \frac{m^{\underline{l}}}{l!}B^{+}_l \\ &=& \frac{1}{1^s} - \frac{1}{m}\sum_{l=0}^{m} \binom{m}{l} B^{+}_l \\ &=& \frac{1}{1^s} - \frac{1}{m}\left(\sum_{l=0}^{m-1} \binom{m}{l} B^{+}_l + B^{+}_m \right) \end{eqnarray}$

となる。さらにベルヌーイ数の漸化式より $\displaystyle \sum_{l=0}^{m-1} \binom{m}{l} B^{+}_l = m$ なので、

$\begin{eqnarray} \zeta(1-m) &=& \frac{1}{1^s} - \frac{1}{m}\left(m + B^{+}_m \right) \\ &=& \frac{1}{1^s} - 1 - \frac{B^{+}_m}{m} \\ &=& - \frac{B^{+}_m}{m} \end{eqnarray}$

となり、ζ(1-m) の値が求められた。

ベルヌーイ数 B^- を使うオイラー・マクローリンの和公式を使った場合、 $\displaystyle \sum_{k=0}^{N-1} \frac{1}{k^s}$ に和公式を適用したあと $N \to \infty$ とすると

$\displaystyle \zeta(s) = - \frac{1}{-s+1}\sum_{l=0}^{M} \frac{(-s+1)^{\underline{l}}}{l!}B^{-}_l + R_M(s)$

が得られる。B⁺ が B^- に変わり、 $\displaystyle \frac{1}{1^s}$ の項が無くなった。
ζ(1-m) についても前と同様の流れで

$\displaystyle \zeta(1-m) = - \frac{1}{m}\left(\sum_{l=0}^{m-1} \binom{m}{l} B^{-}_l + B^{-}_m \right)$

が得られる。B^- の漸化式は場合分けがあったので、この式についても場合分けして考える。
m≧2 のとき、 $\sum_{l=0}^{m-1} \binom{m}{l} B^{-}_l = 0$ となるので、

$\displaystyle \zeta(1-m) = - \frac{B^{-}_m}{m}$

となる。
m=1 のときは $\sum_{l=0}^{0} \binom{m}{l} B^{-}_l = B^{-}_0 = 1$ となることと $B^{-}_1 = -\frac{1}{2}$ より

$\displaystyle \zeta(1-1) = - \frac{1}{1}(1+ B^{-}_1) = -\frac{1}{1}(-B^{-}_1) = \frac{B^{-}_1}{1}$

となり、m≧2 の時の式と符号が違っている。しかし「 m≧2 の時、 B^-_m = (-1)^mB^-_m 」というベルヌーイ数の性質を使えば、

$\displaystyle \zeta(1-m) = (-1)^{m+1} \frac{B^{-}_m}{m}$

のように m=1 の場合も含めた式が得られる。

2025-09-11

メモ: 二種類のベルヌーイ数について

数学整数論

B₁ = 1/2 と B₁ = -1/2
クヌースの定義変更
べき乗和を表す多項式
- ベルヌーイ数の定義式とべき乗和多項式の導出
- べき乗和多項式の微分についての関係式の導出
ベルヌーイ多項式
オイラー・マクローリンの和公式

1. B₁ = 1/2 と B₁ = -1/2

整数論や離散数学その他に登場する数列「ベルヌーイ数」B_nは、B₁ = 1/2 とするものと B₁ = -1/2 とするものの二種類がある。

ベルヌーイ数が現れる文章では、読者が間違えないように「(この本では)B₁ = 1/2 だが、B₁ = -1/2 となる定義を採用するものもある」みたいな注意が記されている場合も多い。

このメモでは以下で二種類のベルヌーイ数の両方に言及することになるので、どちらのベルヌーイ数かをはっきりさせたい時にはBに+や-を付けて、B₁ = 1/2 となるベルヌーイ数をB⁺_nと表記し、B₁ = -1/2 となるベルヌーイ数をB^-_nと表記することにする。

とりあえず、ベルヌーイ数の先頭の値を書き出してみる

とりあえず、ベルヌーイ数の先頭の値を書き出してみると次のようになる。
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c} \hline n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 \\ \hline B^+ & 1 & \frac{1}{2} & \frac{1}{6} & 0 & - \frac{1}{30} & 0 & \frac{1}{42} & 0 & -\frac{1}{30} & 0 & \frac{5}{66} & 0 & -\frac{691}{2730} \\ \hline B^- & 1 & -\frac{1}{2} & \frac{1}{6} & 0 & - \frac{1}{30} & 0 & \frac{1}{42} & 0 & -\frac{1}{30} & 0 & \frac{5}{66} & 0 & -\frac{691}{2730} \\ \hline\end{array}$
知られているように、二種類のベルヌーイ数はn=1以外では値が完全に一致し、またnが3以上の奇数のときはどちらでもB_n=0 となるので、奇数の場合のうちn=1の時だけが異質になっている。

一応、

どちらの定義を採用してもB_nを(-1)ⁿB_nに置き換えることで他方に移る。したがって、すべての公式を読み替えるのは容易であることも注意しておく。
(荒川恒男、伊吹山知義、金子昌信『ベルヌーイ数とゼータ関数』共立出版)

とは言われているし、そもそもベルヌーイ数を見かける機会がそこまで多くはない気がする。それでもどちらのベルヌーイ数を採用するかによって定義式や導出過程の式が違ってくるので、単なる読み替えでは済まず微妙に混乱する。

2. クヌースの定義変更

クヌースの2022年のrecent newsを見ると、クヌースはベルヌーイ数の定義として従来 B₁=-1/2 となるもの(B^-)を採用してきたけど、ピーター・ルシェニー(Peter Luschny)のThe Bernoulli Manifestoを精読した結果、B₁=1/2 のベルヌーイ数(B⁺)を採用することにし、それにともない『The Art of Computer Programming』と『Concrete Mathematics』の該当する箇所も変更したと述べている。*1
ただクヌースにとって一番重要だったのは歴史(ベルヌーイやオイラーはB⁺のベルヌーイ数を用いている)に反していたことだったようなので、B^-の方が便利だという意見がどの程度変わったのかはよく分からない。

3. べき乗和を表す多項式

歴史的には、ベルヌーイ数はべき乗和を表す多項式に関係して登場した。
1からnまでのべき乗の和 $\sum_{k=1}^{n}k^r = 1^r + 2^r + \cdots + n^r$ の値を表す多項式をS⁺_r(n) と書くことにする。これを書き出すと次のようになっている。

$\begin{eqnarray} S^+_0(x) &=& {\bf 1} n \\ S^+_1(x) &=& \frac{1}{2} n^2 &+& {\bf \frac{1}{2}} n \\ S^+_2(x) &=& \frac{1}{3} n^3 &+& \frac{1}{2} n^2 &+& {\bf \frac{1}{6}} n \\ S^+_3(x) &=& \frac{1}{4} n^4 &+& \frac{1}{2} n^3 &+& \frac{1}{4} n^2 &+& {\bf 0} n \\ S^+_4(x) &=& \frac{1}{5} n^5 &+& \frac{1}{2} n^4 &+& \frac{1}{3} n^3 &+& 0 n^2 &{\bf -} & {\bf \frac{1}{30}} n \\ S^+_5(x) &=& \frac{1}{6} n^6 &+& \frac{1}{2} n^5 &+& \frac{5}{12} n^4 &+& 0 n^3 &-& \frac{1}{12} n^2 &+& {\bf 0} n \\ S^+_6(x) &=& \frac{1}{7} n^7 &+& \frac{1}{2} n^6 &+& \frac{1}{2} n^4 &+& 0 n^4 &-& \frac{1}{6} n^3 &+& 0 n^2 &+& {\bf \frac{1}{42}}n \\ S^+_7(x) &=& \frac{1}{8} n^8 &+& \frac{1}{2} n^7 &+& \frac{7}{12} n^5 &+& 0 n^5 &-& \frac{7}{24} n^4 &+& 0 n^3 &+& \frac{1}{12}n^2 &+& {\bf 0} n \\ S^+_8(x) &=& \frac{1}{9} n^9 &+& \frac{1}{2} n^8 &+& \frac{2}{3} n^6 &+& 0 n^5 &-& \frac{7}{15} n^5 &+& 0 n^4 &+& \frac{2}{9}n^3 &+& 0n^2 &{\bf -} & {\bf \frac{1}{30}} n \end{eqnarray}$

ここでS⁺_r(n) の1次の項の係数がベルヌーイ数 B⁺_r になる。

一方、1からnまでの和ではなく0からn-1までの和 $\sum_{k=0}^{n-1}k^r = 0^r + 1^r + \cdots + (n-1)^r$ を考えて(ただし0⁰=1 と考える)、この値を表す多項式を S^-_r(n) と書くと、 r=0 の時は S^-₀(x) = S⁺₀(x) = n となり、r≧1 の時は、S^-_r(n) と S⁺_r(n) は n^r の係数の符号だけが異なり、

$\begin{eqnarray} S^-_0(x) &=& {\bf 1} n \\ S^-_1(x) &=& \frac{1}{2} n^2 &{\bf-}& {\bf \frac{1}{2}} n \\ S^-_2(x) &=& \frac{1}{3} n^3 &-& \frac{1}{2} n^2 &+& {\bf \frac{1}{6}} n \\ S^-_3(x) &=& \frac{1}{4} n^4 &-& \frac{1}{2} n^3 &+& \frac{1}{4} n^2 &+& {\bf 0} n \\ S^-_4(x) &=& \frac{1}{5} n^5 &-& \frac{1}{2} n^4 &+& \frac{1}{3} n^3 &+& 0 n^2 &{\bf -} & {\bf \frac{1}{30}} n \\ S^-_5(x) &=& \frac{1}{6} n^6 &-& \frac{1}{2} n^5 &+& \frac{5}{12} n^4 &+& 0 n^3 &-& \frac{1}{12} n^2 &+& {\bf 0} n \\ S^-_6(x) &=& \frac{1}{7} n^7 &-& \frac{1}{2} n^6 &+& \frac{1}{2} n^4 &+& 0 n^4 &-& \frac{1}{6} n^3 &+& 0 n^2 &+& {\bf \frac{1}{42}}n \\ S^-_7(x) &=& \frac{1}{8} n^8 &-& \frac{1}{2} n^7 &+& \frac{7}{12} n^5 &+& 0 n^5 &-& \frac{7}{24} n^4 &+& 0 n^3 &+& \frac{1}{12}n^2 &+& {\bf 0} n \\ S^-_8(x) &=& \frac{1}{9} n^9 &-& \frac{1}{2} n^8 &+& \frac{2}{3} n^6 &+& 0 n^5 &-& \frac{7}{15} n^5 &+& 0 n^4 &+& \frac{2}{9}n^3 &+& 0n^2 &{\bf -} & {\bf \frac{1}{30}} n \end{eqnarray}$

のようになり、これらの S^-_r(n) の1次の項の係数がベルヌーイ数 B^-_r になる。

さらにこれらのべき乗和多項式 S⁺(x)、S^-(x) は、ベルヌーイ数を使って次のように書き直すことができる。

$\begin{eqnarray} S_0(x) &=& B_0 n \\ S_1(x) &=& \frac{1}{2}B_0 n^2 &+& B_1 n \\ S_2(x) &=& \frac{2}{3\cdot 2}B_0 n^3 &+& \frac{2}{2}B_1 n^2 &+& B_2 n \\ S_3(x) &=& \frac{3\cdot2}{4\cdot3\cdot 2}B_0 n^4 &+& \frac{3\cdot2}{3\cdot2}B_1 n^3 &+& \frac{3}{2}B_2 n^2 &+& B_3 n \\ S_4(x) &=& \frac{4\cdot3\cdot2}{5\cdot4\cdot3\cdot 2}B_0 n^5 &+& \frac{4\cdot3\cdot2}{4\cdot3\cdot2}B_1 n^4 &+& \frac{4\cdot3}{3\cdot2}B_2 n^3 &+& \frac{4}{2}B_3 n^2 &+& B_4 n \\ S_5(x) &=& \frac{5\cdot4\cdot3\cdot2}{6\cdot5\cdot4\cdot3\cdot 2}B_0 n^6 &+& \frac{5\cdot4\cdot3\cdot2}{5\cdot4\cdot3\cdot2}B_1 n^5 &+& \frac{5\cdot4\cdot3}{4\cdot3\cdot2}B_2 n^4 &+& \frac{5\cdot4}{3\cdot2}B_3 n^3 &+& \frac{5}{2}B_4 n^2 &+& B_5 n \end{eqnarray}$

ベルヌーイ数とべき乗和多項式の導出

べき乗和の値を表す多項式 S⁺_r(x) と S^-_r(x) はどちらについても、「S_r(x) をxで微分して定数項(ベルヌーイ数B_r)を省いたものは、S_r-1(x) のr倍になる」という性質がある。つまり、

${S^{+}_{r}}'(x) - B^+_r = r S^+_{r-1}(x) \\ {S^{-}_{r}}'(x) - B^-_r = r S^-_{r-1}(x)$

が成り立っている。( $\sum_{k=1}^{n}k^r$ や $\sum_{k=0}^{n-1}k^r$ は n が自然数の時しか意味を持たない式なので n での微分を考えることができないけれど、べき乗和多項式 S⁺(n)、 S^-(n) は多項式なので変数 n に自然数以外の実数を与えることができ微分を考えられる)。
この性質が成り立つことを使うと、べき乗和多項式とベルヌーイ数の値を導出していくことができる。
最初に、自然数の0乗 (=1) の和を表す多項式S⁺(x)、S^-(x) を考えると

$S^+_0(n) = B^+_{0}n \quad S^+_0(1) = 1 \\ S^-_0(n) = B^-_{0}n \quad S^-_0(1) = 1$

なので、B⁺₀ = 1 、B^-₀ = 1 と値が決まる。あとは

$\displaystyle S^+_{r+1}(n) = (r+1)\int_0^{n}S^+_r(x) dx + B^+_r n \qquad S^+_{r+1}(1) = 1 \\ \displaystyle S^-_{r+1}(n) = (r+1)\int_0^{n}S^-_r(x) dx + B^-_r n \qquad S^-_{r+1}(1) = 0$

を繰り返し使う(r乗和多項式を「r+1倍して」「積分して」「1次の項を付け加え」「1次の係数を決める」とr+1乗和多項式が得られる)ことで、高次のべき乗和多項式とベルヌーイ数の値を計算していくことができる。
例えばB⁺の場合、まず

$\displaystyle S^+_{1}(n) = \int_0^{n}S^+_0(x) dx + B^+_1 n = \frac{1}{2}B^+_0 n^2 + B^+_1 n$

となり、S⁺₁(1) = 1 となることから、 $\displaystyle B^+_1 = \frac{1}{2}$ と決まり、 S⁺₁(n) の各係数の値も決まる。次は

$\displaystyle S^+_{2}(n) = 2 \int_0^{n}S^+_1(x) dx + B^+_2 n = \frac{1}{3}B^+_0 n^3 + B^+_1n^2 + B^+_2 n$

となり、S⁺₂(1) = 1 となることから、 $\displaystyle B^+_2 = \frac{1}{6}$ と計算できる。以下同様にして、べき乗和の式とベルヌーイ数の値が並行して求まっていく。

一般的な式の形を求めると、S^±_r(x) のk次の係数を c^±_r,k と書くと、 $\displaystyle S^{\pm}_{r}(n) = r\int_0^{n}S^{\pm}_{r-1}(x) dx + B^{\pm}_{r-1} n$ の左辺と右辺の係数の比較を繰り返し使って

$\displaystyle c^{\pm}_{r,k} = \frac{r}{k} c^{\pm}_{r-1, k-1} = \frac{r(r-1)}{k(k-1)}c^{\pm}_{r-2,k-2} = \cdots = \frac{r(r-1)\cdots(r-k+2)}{k(k-1)\cdots 2} c^{\pm}_{r+1-k, 1} \\ \displaystyle \quad = \frac{1}{r+1}\binom{r+1}{k}B^{\pm}_{r+1-k}$

と値が分かるので、べき乗和多項式を

$\displaystyle S^{\pm}_{r}(n) = \frac{1}{r+1} \sum_{k=1}^{r+1}\binom{r+1}{k}B^{\pm}_{r+1-k} n^k = \frac{1}{r+1} \sum_{i=0}^{r}\binom{r+1}{i}B^{\pm}_{i} n^{r+1-i}$

のようにベルヌーイ数を使った形で表すことができる。
ベルヌーイ数についても、B⁺の場合は S⁺(1) = 1 になることから、

$\displaystyle \sum_{k=1}^{r+1}\binom{r+1}{k}B^{+}_{r+1-k} n^k = r+ 1$

というベルヌーイ数について成り立つ漸化式(ベルヌーイ数の定義にもよく使われる式)が得られる。
B^-の場合もほぼ同様で、S^-(1) = 0 から、

$\displaystyle \sum_{k=1}^{r+1}\binom{r+1}{k}B^{-}_{r+1-k} n^k = 0$

の漸化式が得られるけど、こちらの式は r=0 の場合には成り立たないので、r=0の場合を別立てにして B^-₀ = 1 としないといけない。

べき乗和多項式の微分についての関係式の導出

上でベルヌーイ数の値やべき乗和の式を導くときに

$\displaystyle {S^{\pm}_{r}}'(x) - B^{\pm}_r = r S^{\pm}_{r-1}(x)$

という関係式を使った。この関係式は次のようにして出てくる。
nが自然数の時、

$\begin{eqnarray} {S^{+}_{r}}(n) & = & 1 + \cdots + (n-1)^r + n^r \\ {S^{+}_{r}}(n-1) & = & 1 + \cdots + (n-1)^r \end{eqnarray}$

なので、左辺と右辺それぞれ差を取って

$\displaystyle S^+_r(n) - S^+_r(n-1) = n^r$

となる。この等式は左辺と右辺の両方とも多項式で n=0、1、2、3…(全ての自然数)で成り立っているので、(k次の多項式はk+1個の値で等しければ同じ多項式になるので)自然数nの時だけでなく任意の実数xで成り立つ。自然数だけでなく実数で成り立つ式なので、記号を変えて

$\displaystyle S^+_r(x) - S^+_r(x-1) = x^r$

と書いておく。この両辺をxで微分すると、

$\displaystyle {S^+_r}'(x) - {S^+_r}'(x-1) = r x^{r-1}$

という式が得られる。
この式から x=1、2、3、…、n を代入したn個の式を作ってそれらの和を取る。
すると左辺については値が打ち消しあって S⁺_r'(n) と S⁺'(0) だけが残り、右辺については「1^r-1 から n^r-1までの和」(= S⁺_r-1(n))の r 倍になる。ここで S⁺_r'(0) は、S⁺_r(x) の1次の項の係数なので B⁺_r となり、

$\displaystyle {S^{+}_{r}}'(n) - B^{+}_r = r S^{\pm}_{r-1}(n)$

という関係式が得られ、この関係式も自然数だけでなく任意の実数で成り立つ関係式になる。(上の流れできちんと証明するには、1からnまでのr乗和の値が(r+1次の)多項式で表せることも証明しておかないといけない)。

S^-_r(x) についても、 $\displaystyle S^-_r(x+1) - S^-_r(x) = x^r$ の関係から始めて

$\displaystyle {S^{-}_{r}}'(x) - B^{-}_r = r S^{-}_{r-1}(x)$

の関係を導くことができる。

4. ベルヌーイ多項式

べき乗和多項式の形を導出する時にべき乗和多項式の微分を考えることが役に立ったのだけれど、べき乗和多項式を微分して得られる多項式

$\displaystyle B_r(x) \quad = {S^{+}_r}'(x-1) \quad = {S^{-}_r}'(x)$

は、「ベルヌーイ多項式」と呼ばれる。
ここだけ見ると S⁺(x) を使うより S^-(x) を使う方が綺麗な感じがある。
$S^+_r(x) - S^+_r(x-1) = S^-_r(x+1) - S^-_r(x) = x^r$ の関係から

$\displaystyle \int_{x-1}^{x} {S^{+}_r}'(x) dx= \int_x^{x+1}{S^{-}_r}'(x) dx = x^r$

となっているので、積分との関係を考えると「B_r(x) = S⁺'(x-1)」の方が良い式なのだと思う。

このベルヌーイ多項式B_r(x)を使うとベルヌーイ数は、

$B^{-}_r = B_r(0) \\ B^{+}_r = B_r(1)$

となり、うまい具合に(悪い具合に?) B⁺ と B^- のどちらも同じような式で表すことができる。(当然、r=1 の時だけ B_r(0) ≠ B_r(1) となる)。

5. オイラー・マクローリンの和公式

思ったより長くなったのでオイラー・マクローリンの和公式の部分は別に分けることにする。

⇒『メモ: 二種類のベルヌーイ数について(続き): オイラー・マクローリンの和公式』

*1:『Concrete Mathematics』の翻訳『コンピュータの数学』は出版のタイミングが微妙に恵まれていないように感じる。まず『Concrete Mathematics』第1版が1989年に出て『コンピュータの数学』第1版は1993年に出ているけど、翌年1994年に『Concrete Mathematics』の第2版が出ている。第2版は5.8節が追加された以外はどこをどの程度直しているのかよく分からないから改訂版としてのインパクトがあまりないしタイミング的な理由もあって当時は翻訳・出版が行われなかったのだろう。その後2020年に『コンピュータの数学』第2版が出たけれど、今度は2022年というタイミングで『Concrete Mathematics』に大きな変更がされることになった(ベルヌーイ数の定義変更のよる修正ページが40ページ以上ある)。

2022-05-21

素数定理の証明について

数学整数論

素数定理の証明については、ザギエ(Zagier)による4ページの解説論文「Newman's Short Proof of the Prime Number Theorem」に示されている証明があるけど、説明が簡潔すぎることもあって証明を読み進んでいくのがかなり大変という印象がある。

むしろ、アダマールとド・ラ・ヴァレ・プーサンによる素数定理の最初の証明の方が、きちんと正しく証明するのは非常に難しいにしても、やりたい事は分かりやすい気がする。

またザギエが参照しているコレヴァ(Korevaar)の解説論文を見てみると、ザギエの提示している証明の背後には、ウィーナー・池原の定理による証明が存在していることが分かる。*1

なので、その辺りのことをまとめておく。

1. チェビシェフ関数の性質

1.1. 第1チェビシェフ関数θ(x)、第2チェビシェフ関数ψ(x)

アダマールやド・ラ・ヴァレ・プーサンによる証明も、ウィーナー・池原の定理を用いる証明も、ザギエの証明も、いずれもチェビシェフ関数を利用しているので、その説明からおこなう。(ちなみにニューマンの論文では素数定理の証明を2つ示しているけれど、どちらもチェビシェフ関数を使うのとは別の経路で素数定理を証明している。)

第1チェビシェフ関数θ(x)は、

θ(x) = 「x以下の全ての素数pに対する自然対数log p の和」

と定義される。これは、

$\theta(x) = \sum\limits_{\substack{p\\p \le x }} \log p$

のように書くこともできる。(和の添字にpを使ったときは、pは素数だけを渡るとする)。
例えばθ(10)を考える。10より小さい素数は、2、3、5、7、なので、

θ(10) = log2 + log3 + log5 + log7

となる。

一方、第2チェビシェフ関数ψ(x)は、x以下の素数だけでなく、x以下の数で「素数のべき乗になる数 p^m」に対しても、log p を足す。これは、

$\psi(x) = \sum\limits_{\substack{p ,m\\p^m \le x }} \log p$

と書くこともできる。(ここでpは素数、mは正整数を動く。)
例えば ψ(10)を考えると、10より小さい数で、素数、または、素数のべき乗になっている数は、

2、3、4(=2^2)、5、7、8(=2^3)、9(=3^2)

なので、

ψ(10) = log2 + log3 + log2 + log5 + log7 + log 2 + log3

となり、θ(10)と比べると、4、８、9に対するlog2、 log2、log3のぶんだけだけ大きくなっている。

1.2. チェビシェフ関数と素数定理

さて、素数定理の証明の観点から重要なのは、

θ(x) ～ x

あるいは、

ψ(x) ～ x

が成り立てば、そこから素数定理

$\pi(x) \sim \frac{x}{\log x}$

が導かれる、ということ。(ここで f(x)～g(x) は、 $\lim\limits_{x\to\infty}\frac{f(x)}{g(x)}=1$ を表す。)
実際、アダマールとド・ラ・ヴァレ・プーサンは、第2チェビシェフ関数ψ(x)について ψ(x)～x を示すことで素数定理を証明した。

1.3. チェビシェフ関数とゼータ関数の関係

素数定理の証明では、ゼータ関数の性質が重要な役割を果たす。
まず第2チェビシェフ関数ψ(x)とゼータ関数ζ(s)の間には、

$\displaystyle{-\frac{\zeta'(s)}{\zeta(s)} = s\int_{1}^{\infty}\frac{\psi(x)}{x^{s+1}}dx}$

の関係がある。アダマールとド・ラ・ヴァレ・プーサンによる素数定理証明はフォン・マンゴルトの明示公式にもとづいたものだけど、その明示公式はこの関係式から出発して導かれる。またウィーナー・池原の定理を用いる証明では、この関係式にウィーナー・池原の定理を適用する。
一方、第1チェビシェフ関数θ(x)とゼータ関数の関係はもう少しだけ複雑で、同様の形の変換をほどこすと、-ζ'(s)/ζ(s)の代わりに $\Psi(s) = \sum\limits_{p} \frac{\log p}{n^p}$ というディリクレ級数(ここで和の添字pは全ての素数を渡る)で定義される関数に変換され、

$\Psi(s) =\quad \displaystyle{-\frac{\zeta'(s)}{\zeta(s)} - \sum\limits_{p}\frac{\log p}{p^s(p^s-1)} \quad= s\int_{1}^{\infty}\frac{\theta(x)}{x^{s+1}}dx}$

という関係になっている。ザギエの証明は、第2チェビシェフ関数ではなく、第1チェビシェフ関数を使っているので、そのぶん素数定理とゼータ関数との関係は少し分かりにくくなっているような感じがする。

2. フォン・マンゴルトの明示公式と、アダマールとド・ラ・ヴァレ・プーサンによる証明

アダマールとド・ラ・ヴァレ・プーサンによる素数定理の証明では、チェビシェフ関数に対するフォン・マンゴルトの明示公式が重要な役割を果たしている。(フォン・マンゴルトが明示公式を証明したのが1895年。アダマールとド・ラ・ヴァレ・プーサンがそれぞれ独立に素数定理を証明したのが1896年)
導出過程などは略して明示公式を示すと、第2チェビシェフ関数ψ(x)(を不連続点で少し修正した関数)が、フォン・マンゴルトの明示公式では

$\psi(x) = x - \sum\limits_{\rho}\frac{x^{\rho}}{\rho} - \log(2\pi) -\frac{1}{2}\log\left(1-\frac{1}{x^2}\right)$

のように表される。ここで和の「ρ」はゼータ関数ζ(s)の0≦Re(s)≦1の範囲にある全ての零点を渡る。
素数定理を示すには「ψ(x)～x」すなわち $\lim\limits_{x\to\infty}\frac{\psi(x)}{x} =1$ を示せば良かったけど、明示公式のうちゼータ関数の零点についての和以外の部分を見ると、

$\displaystyle{\lim\limits_{x\to\infty}\frac{x - \log(2\pi) -\frac{1}{2}\log\left(1-\frac{1}{x^2}\right)}{x} = 1}$

となっている。なので、あとは

$\displaystyle{\lim\limits_{x\to\infty}\frac{\sum\limits_{\rho}\frac{x^{\rho}}{\rho} }{x}=0}$

が言えれば、素数定理が証明できたことになる。
ここで、ゼータ関数の零点ρ=a+ibを適当に一つ取って、

$\displaystyle{\lim\limits_{x\to\infty}\frac{\frac{x^{\rho}}{\rho}}{x} = \lim\limits_{x\to\infty}\frac{x^{\rho-1}}{\rho} = \lim\limits_{x\to\infty}\frac{x^{(a-1)+ib}}{\rho}}$

の値を考える。xは実数で、実数の虚数乗は絶対値が1だから、x^ibの部分は絶対値が1。なので、もしもρの実部Re(ρ)=a<1 ならば、 $\lim\limits_{x\to\infty}\frac{x^{\rho}/\rho}{x} =0$ となる。
ということは、あとは 0≦Re(s)≦1の範囲にある全ての零点ρがRe(ρ)<1であることが言えれば(そのためにはRe(s)=1でζ(s)≠0となることが言えればいい)素数定理が証明される?

残念ながらこれは成り立たない。0≦Re(s)≦1の範囲にあるゼータ関数の零点は無限個あり、しかも $\sum\limits_{\rho}\frac{x^{\rho}}{\rho}$ は条件収束しかしていないので、各項をxで割ったものが0に収束することが言えても、和全体をxで割ったものが0に収束することは言えない。
とはいえ、アダマールもド・ラ・ヴァレ・プーサンも、和の極限に関するこの問題をうまく回避し、なおかつRe(s)=1でζ(s)≠0 となることも証明して、素数定理を証明することに成功した。

3. ウィーナー・池原の定理による証明

3.1. メリン変換

アダマールもド・ラ・ヴァレ・プーサンも、フォン・マンゴルトの明示公式(を和の極限の困難をさけるために修正したもの)を使って素数定理を証明している。しかし、導出過程をきちんと正当化しつつ明示公式を導くのは非常にたいへん。
なので明示公式を使わない証明があるとうれしい。
そこでまず、明示公式に至る前の $-\frac{\zeta'(s)}{\zeta(s)} = s\int_{1}^{\infty}\frac{\psi(x)}{x^{s+1}}dx$ 、あるいは $\Psi(s) = s\int_{1}^{\infty}\frac{\theta(x)}{x^{s+1}}dx$ の形の積分

$\displaystyle{ g(s) = s\int_{1}^{\infty}\frac{f(x)}{x^{s+1}}dx}$

について調べてみる。これはメリン変換と呼ばれる形の積分。(1/xを新しい変数にして変数変換して積分範囲も変えると、「メリン変換」で通常提示される形になる。)
まず f(x) = cx として、メリン変換 g(s) を計算してみると、

$\displaystyle{ g(s) = \frac{c}{s-1} + c} \quad(\mbox{Re}(s)>1)$

となる。またここで積分の下端1を別の値にしてみると、

$\displaystyle{ s\int_{A}^{\infty}\frac{cx}{x^{s+1}}dx} = \frac{c}{s-1}+\mbox{定数}\quad(\mbox{Re}(s)>1)$

となっている。積分の下端Aをどれだけ大きな数にしてもこうなるのて、xが大きい部分での積分結果が $\frac{c}{s-1}$ の部分に集約されているように見える。
次にf(x)として、f(x)～cxであるような任意の関数f(x)を取ってみる。するとこの場合もRe(s)>1で積分できて、右側からs=1に近づいていくと、 $g(s)=\frac{c}{s-1}+O(1)$ となる。(つまりs→1のとき g(s)≒ $\frac{c}{s-1}$ のように振舞う。)
例えば、f(x) = ⌊x⌋ (= x以下の最大整数)とすると、f(x)～x で、 $s\int_{1}^{\infty}\frac{\lfloor x \rfloor}{x^{s+1}}dx=\zeta(s)$ で、ζ(s)はs=1に留数1の1位の極を持つのでs→1でζ(s)≒ $\frac{1}{s-1}$ が成り立っている。

では逆に「s→1のときに g(s)≒ $\frac{c}{s-1}$ のように振舞うなら f(x)～cx」が言えるか?
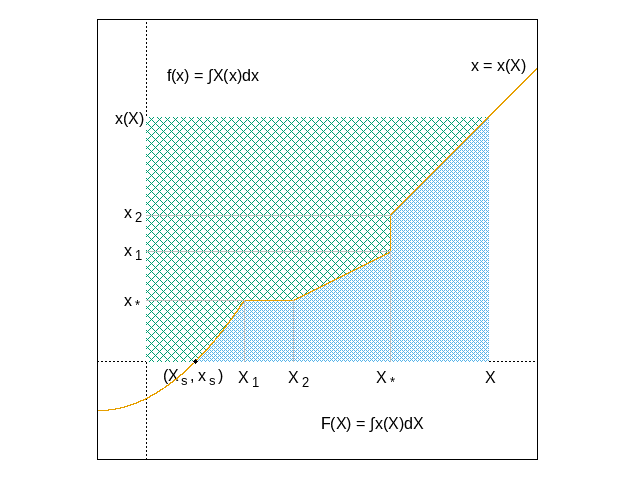
というとこれは成り立たない。例えば、

$f(x) = 2^k \quad \left(2^{k-1}\le x \lt 2^{k}\right)$

という関数を考える。これはy=xのグラフとy=2xのグラフの間を階段状に増加していく関数なので、特定のcxには漸近しない。しかし、このf(x)からg(s)を計算すると、

$\displaystyle{g(s) = 2\frac{1-2^{-s}}{1-2^{1-s}}} \quad(\mbox{Re}(s)>1)$

となり、s→1のとき、 $g(s) = \frac{1}{\log 2}\frac{1}{s-1} + O(1)$ のように振舞う(はず。計算ミスがなければ。)

とはいえ、 $g(s) = s\int_{1}^{\infty}\frac{f(x)}{x^{s+1}}dx$ が、s→1で g(s)≒ $\frac{c}{s-1}$ のように振舞うことと、なんらかの補助的な条件から、f(x)～cx を導けないだろうか。

それを助けてくれるのが、ウィーナー・池原の定理。

3.2. ウィーナー・池原の定理

ウィーナー・池原の定理を、ここでの話に合わせた形で提示すると、次のようになる。

ウィーナー・池原の定理
f(x)は、x≧1で非負かつ非減少な関数であり、そのメリン変換
$\displaystyle{ g(s) = s\int_{1}^{\infty}\frac{f(x)}{x^{s+1}}dx}$

は、Re(s)>1で存在するとする。このとき、関数 $g(s) - \frac{c}{s-1}$ を Re(s)≧1 の範囲に連続関数として拡張できるなら、
$\lim\limits_{x\to \infty}\frac{f(x)}{x} = c$

が成り立つ。(つまり f(x)～cx が成り立つ。)

例えば、f(x)として先に例として出したy=xとy=2xの間を階段状に増加する関数(cxに漸近しない関数)を取ると、 $g(s) = 2\frac{1-2^{-s}}{1-2^{1-s}}$ だったので、境界線Re(s)=1に右から近づいたとき、s→1だけでなく、 $s\to 1+\frac{2\pi n}{\log 2} i$ の時にも発散するため、ウィーナー・池原の定理の条件「 $g(s) - \frac{c}{s-1}$ を Re(s)≧1 の範囲に連続関数として拡張できる」を満たすことができない。

3.3. ウィーナー・池原の定理を用いた素数定理の証明

ウィーナー・池原の定理を素数定理の証明に適用するためには、g(s)を

$g(s) = s\int_{1}^{\infty}\frac{\psi(x)}{x^{s+1}}dx = \displaystyle{-\frac{\zeta'(s)}{\zeta(s)}}$

として、必要な性質を満たしていることを見る必要がある。

まずRe(s)>1の範囲で $g(s) = s\int_{1}^{\infty}\frac{\psi(x)}{x^{s+1}}dx$ が値を持つ必要がある。(例えばf(x)=x²だと、Re(s)>2でないと積分が発散する。)
これを言うには「ψ(x) = O(x)」(ψ(x)の増加が、xの定数倍より遅い)を証明すればいい。

あとは、 $-\frac{\zeta'(s)}{\zeta(s)} - \frac{1}{s-1}$ の、Re(s)=1上での様子(連続かどうか)が問題となる。
ζ(s)が零点か極になるsでは、-ζ'(s)/ζ(s)は極を持ち、それ以外の点では-ζ'(s)/ζ(s)は正則になることに注意して考える。(ここで、素数定理の最初の証明で示された「Re(s)=1でζ(s)≠0」が使われる。)
まずゼータ関数ζ(s)の極を見る。ζ(s)はs=1に1位の極を持っていて、 $\zeta(s) = \frac{1}{s-1} + \cdots$ とローラン展開される。このことから、 $-\frac{\zeta'(s)}{\zeta(s)} = \frac{1}{s-1} + \cdots$ となって -ζ'(s)/ζ(s)もs=1で留数1の1位の極を持つことが分かる。
これでs=1のことが分かったので、Re(s)=1の直線上のs=1以外の点での -ζ'(s)/ζ(s) の様子が問題となる。素数定理の最初の証明で示されたように、Re(s)=1ではζ(s)≠0だった(そしてζ(s)はs=1以外には極を持たない)。なので、-ζ'(s)/ζ(s)はRe(s)=1の直線上でs=1を除いて正則になる。よって $-\frac{\zeta'(s)}{\zeta(s)} - \frac{1}{s-1}$ は、Re(s)=1の直線上全体で正則となるので、Re(s)=1上で連続。
こうして、ζ(s)がRe(s)=1でζ(s)≠0であること(とs=1で極を持つこと)から、ψ(x)と -ζ'(s)/ζ(s) がウィーナー・池原の定理の適用条件を満たしていることが導かれる。
したがってウィーナー・池原の定理を適用することで、ψ(x)～xが言え、素数定理が証明される。

4. ニューマン・コレヴァ・ザギエの証明

4.1. コレヴァの証明

ニューマンは、コーシーの積分定理をうまく用いて補助的な定理を証明し、それを使って素数定理の証明を大幅に簡略化した。
しかしニューマン自身の証明は、チェビシェフ関数を使うのとは異なる仕方の証明なので、ここではニューマンの証明を分析したコレヴァによる証明を見る。
まずコレヴァは、ニューマンが用いた手法によって次の補助定理が証明できることから始める。(この補助定理はザギエの証明でも使われる。コレヴァの論文では「Auxiliary Tauberian theorem」と呼ばれ、ザギエの論文では「Analytic Theorem」と呼ばれている。)

補助定理: 関数F(t) (t≧0) は有界で、任意の有界閉区間で積分できるとする。このとき
$G(z) = \int_{0}^{\infty}F(t)e^{-zt}dt$

は、Re(z)>0で正則。
(註: Re(z)>0のときは、tが大きくなるとき $|e^{-zt}|$ が小さくなっていき、 $\int_{0}^{\infty}F(t)e^{-zt}dt$ はうまく収束してくれる。しかし $\int_{0}^{\infty}F(t)dt$ は収束するとは限らない。そしてz→0のときに $\int_{0}^{\infty}F(t)e^{-zt}dt$ が収束したとしても、その時 $\int_{0}^{\infty}F(t)dt$ が収束するとは限らない。)
このG(z)が、Re(s)≧0まで解析接続できるとする。
このとき、 $\int_{0}^{\infty}F(t)dt$ は収束し、
$\int\limits_{0}^{\infty}F(t)dt = G(0) = \lim_{z\to 0}G(z)$

が成り立つ。

コレヴァは次に、この定理から、弱い形のウィーナー・池原の定理を導く。「弱い」というのは、定理の適用条件が元の定理より厳しくなっているからで、元の定理で「 $g(s) - \frac{c}{s-1}$ を、Re(s)≧1まで連続関数として拡張できる」という条件だったところが、「 $g(s) - \frac{c}{s-1}$ を、Re(s)≧1まで解析接続できる」というもっと強い条件に置き換わる。
弱い形のウィーナー・池原の定理は、おおよそ次のように導かれる。 $g(s) - \frac{c}{s-1}$ は、

$g(s) - \frac{c}{s-1} = s\int_{1}^{\infty}\frac{f(x)}{x^{s+1}}dx - \frac{c}{s-1} = s\int_{1}^{\infty}(\frac{f(x)}{x}-c )\frac{dx}{x^{s}} +c$

と書き換えることができる。*2
$x=e^{t}$ で変数を変換すると、

$g(s) - \frac{c}{s-1} = s\int_{0}^{\infty}(\frac{f(e^t)}{e^t}-c )e^{-(s-1)t}dt +c$

となる。さらに $s-1=z$ とすると、

$g(z+1) - \frac{c}{z} = (z+1)\int_{0}^{\infty}(\frac{f(e^t)}{e^t}-c )e^{-zt}dt +c$

となる。この式の積分のところに補助定理を適用することができる。(「 $g(s) - \frac{c}{s-1}$ をRe(s)≧1まで解析接続できる」ことから、「 $G(z)=\int_{0}^{\infty}(\frac{f(e^t)}{e^t}-c )e^{-zt}dt$ をRe(z)≧0まで解析接続できる」ことが言え、補助定理の適用条件が満たされる。)
よって補助定理により $\int_{0}^{\infty}(\frac{f(e^t)}{e^t}-c )dt$ は収束する。 $e^{t}=x$ で変数をxにすると、
$\int_{1}^{\infty}(\frac{f(x)}{x}-c )\frac{1}{x}dx$ となり、この積分が収束することから、 $\frac{f(x)}{x}\to c$ を導くことができる。このように補助定理から弱い形のウィーナー・池原の定理が証明される。

そして $-\frac{\zeta'(s)}{\zeta(s)} - \frac{1}{s-1}$ は「Re(s)≧1まで解析接続できる」の条件を満たしているので、弱いウィーナー・池原の定理を適用できて、それにより素数定理が証明される。
これがコレヴァによる証明の道筋。

4.2. ザギエの証明での変更点

ザギエが解説論文で示している証明は、コレヴァの証明をいくらか修正したものになっている。
まず一点目として、ザギエは第2チェビシェフ関数ψ(x)ではなく第1チェビシェフ関数θ(x)を使って証明をおこなっている。
これは、第1チェビシェフ関数のメリン変換

$\displaystyle{ \Psi(s) = s\int_{1}^{\infty}\frac{\theta(x)}{x^{s+1}}dx}$

にもウィーナー・池原の定理が適用できるため。 $\Psi(s) = -\frac{\zeta'(s)}{\zeta(s)} - \sum_{p}\frac{\log p}{p^s(p^s-1)}$ で、 $\sum_{p}\frac{\log p}{p^s(p^s-1)}$ の部分は、Re(s)=1を含む適当な範囲で正則なため、定理の適用条件には影響を与えないので。

二点目として、コレヴァのように補助定理から弱いウィーナー・池原の定理を一般的に導くのではなく、第1チェビシェフ関数θ(x)を含んだ式に直接補助定理を適用して、θ(x)～x を示している。

コレヴァは一般的な $F(t) = e^{-t}f(e^t)-c$ と $G(z)=\frac{g(z+1)}{z+1}-\frac{c}{z}$ に補助定理を適用して、そこから f(x)～cx が成り立つことを示し、 $g(s) = s\int_{1}^{\infty}\frac{f(x)}{x^{s+1}}dx$ に対する弱いウィーナー・池原の定理を証明する。

ザギエは、一般的なf(x)ではなく、 $F(t) = e^{-t}\theta(e^t)-1$ と $G(z)=\frac{\Psi(z+1)}{z+1}-\frac{1}{z}$ に補助定理を直接適用し、その結果を使ってθ(x)～xを証明する。

4.3. ザギエの証明でやらないといけないこと

最終的に、ザギエによる証明では、何を行う必要があるのか?

[1] 補助定理の証明

ニューマンの手法によってコーシーの積分定理を使って補助定理を証明する、というのがコレヴァ・ザギエの証明のキーポイントになる。

次に、 $F(t) = e^{-t}\theta(e^t)-1$ と $G(z)=\frac{\Psi(z+1)}{z+1}-\frac{1}{z}$ が補助定理の条件を満たしている事を示さないといけない。(以下の[2]～[5])。
まず、 $F(t) = e^{-t}\theta(e^t)-1$ が有界でないといけない。(この条件はウィーナー・池原の定理での「メリン変換がRe(s)>1で存在する」に対応する。) それを示すために「θ(x) = O(x)」の証明がいる。

[2] θ(x) = O(x)　(ザギエ定理III)

そして、 $G(z)=\frac{\Psi(z+1)}{z+1}-\frac{1}{z}$ がRe(z)≧0で正則であることを示さないといけない。 $G(z) = \frac{1}{z+1}\left(\Psi(z+1)-\frac{1}{z}\right)+\frac{1}{z+1}$ となるので、 $\Psi(s)-\frac{1}{s-1}$ がRe(s)≧1で正則であること(これは弱いウィーナー・池原の定理の適用条件にほかならない)を証明すればよい。 $\Psi(s) -\frac{1}{s-1}=\left(-\frac{\zeta'(s)}{\zeta(s)} -\frac{1}{s-1}\right) - \sum\limits_{p}\frac{\log p}{p^s(p^s-1)}$ なので、本質的にはゼータ関数ζ(s)の性質を証明することになる。
まずζ(s)がs=1で留数1の1位の極を持ち、その点を除けば、Re(s)≧1を含む適当な領域で、ζ(s)が正則になる、という性質の証明をする。

[3] Re(s)>1で、ζ(s)が定義できる。　(ザギエ定理I)
[4] $\zeta(s)-\frac{1}{s-1}$ を、Re(s)>0まで、正則関数として拡張できる。　(ザギエ定理II)

あとは、Re(s)≧1でζ(s)≠0となることが言えれば、 $-\frac{\zeta'(s)}{\zeta(s)}-\frac{1}{s-1}$ がRe(s)≧1で正則であることが言え、そこから $\Psi(s)-\frac{1}{s-1}$ もRe(s)≧1で正則であることが言える。

[5] Re(s)≧1で、ζ(s)≠0かつ $\Psi(s)-\frac{1}{s-1}$ は正則である。　(ザギエ定理IV)

これでG(z)がRe(s)≧0で正則になることが言え、補助定理が適用でき、
$\displaystyle{\int\limits_{0}^{\infty}F(t)dt=\int\limits_{0}^{\infty}\left(e^{-t}\theta(e^t)-1\right)dt=\int\limits_{1}^{\infty} \frac{\theta(x)-x}{x^2}dx}$
が有限値に収束することが証明される。

[6] $\int_1^{\infty}\frac{\theta(x)-x}{x^2}dx$ は収束する。　(ザギエ定理V)

θ(x)～x というのは $\lim\limits_{x\to \infty}\frac{\theta(x)-x}{x}=0$ と等しいけど、これが $\int_1^{\infty}\frac{\theta(x)-x}{x^2}dx$ が収束することから導かれる。

[7] θ(x)～x　(ザギエ定理VI)

そしてθ(x)～xから素数定理が導かれる。
ザギエは、以上の補助定理と定理I～VIの証明、素数定理の解説を4ページにまとめて提示している。

5. 参考文献

D. J. Newman, Simple Analytic Proof of the Prime Number Theorem(1980)
J. Korevaar, On Newman's Quick Way to the Prime Number Theorem(1982)
D. Zagier, Newman's Short Proof of the Prime Number Theorem(1997)
河田敬義『数論―古典数論から類体論へ』岩波書店(1992)
INTEGERS「素数定理の証明」

*1:ザギエの論文のタイトルは「Newman's Short Proof of the Prime Number Theorem」だけど、ニューマン自身の証明とはかなり違っていて、むしろコレヴァの解説論文「On Newman's Quick Way to the Prime Number Theorem」の証明を元にしている。

*2:ここで「sに1を代入すると「g(s)-c/(s-1)」が(Re(s)≧0まで解析接続できるから)有限値になるので、∫₀^∞(f(x)/x-c)/x dx も有限値になる」と進んでいくことはできない。もとの積分が発散せず定義されていたのはRe(s)＞0のときで、この積分がs→1の時に有限値になることが分かっても、直接s=1を代入した時にも発散せず有限値になるかどうかは分からない。

2021-05-13

ルジャンドル変換についてのメモ

数学物理

まずルジャンドル変換というのは、おおざっぱには次のようなもの。

xを変数とする関数f(x)とその導関数 $X(x) = \frac{df(x)}{dx}$ を考える。(この関数f(x)は適当な性質を満たす(= 凸関数である)としておく。)
このとき、X = X(x)の関係を逆に解いて(x = x(X)という関数を導いて)、xの代わりにXを独立変数にして、
$F(X) = \left( \frac{df}{dx} \cdot x - f \right)(X)$
という新しい関数を作る。このとき $x(X) = \frac{dF(X)}{dX}$ の関係が成り立っている。
このようにf(x) (と $X(x) = \frac{df(x)}{dx}$ )から、F(X)を得る操作をルジャンドル変換という。
また逆に、F(X) (と $x(X) = \frac{dF(X)}{dX}$ )にルジャンドル変換をおこなうと、
$\left( \frac{dF}{dX} \cdot X - F \right)(x) = f(x)$
となりf(x)が戻ってくる。

$f(x) \qquad X = \frac{df(x)}{dx}$
⇅ ルジャンドル変換
$F(X) \qquad x = \frac{dF(X)}{dX}$

単調増加関数の双対性

ルジャンドル変換は、主として凸関数に関する操作なので*1、そこに至る準備として単調増加関数(つまり x≦x'ならf(x)≦f(x')となる関数)を考える。

単調増加関数の入力側をxで表し出力側をXで表すことにする。つまり、x ↦ X のように値が定まっている。
また関数自体も出力と同じXで表記し、X = f(x) のように書かず

X = X(x)

のように書くことにする。

さて関数 X(x) は単調増加関数なので、逆関数がほぼ定まる。
ここで「ほぼ」なのは、

不連続点x_*で関数値が X₁からX₂に不連続に増加したとすると、X₁からX₂の範囲は関数X(x)の値域にならないので、逆関数の側では X₁からX₂までの値について対応するxの値がない。
あるx₁からx₂まで関数値が一定値X_*を取ったとすると、逆関数の側では、X_*に対応するxの点が無数にある。

となるので。
しかし

X₁からX₂までの値には、x_*を対応させる。
X_*に対応する値はx₁とx₂のどちらかにして、関数x(X)の不連続点とする。

と決めてやれば、X(x)の「逆関数」x(X)が決まる。このx(X)も単調増加関数になる。

ここで増加関数X(x)と、その「逆関数」x(X)の間には次のような関係がある。

X(x)	x(X)
単調増加関数	単調増加関数
不連続点x_*で、左極限値X₁から右極限値X₂への不連続な増加。	X₁からX₂まで、一定値x_*を取る。
x₁からx₂まで、一定値X_*を取る。	不連続点X_*で、左極限値x₁から右極限値x₂への不連続な増加。

凸関数の間の双対性

ここで、さらに関数X(x)と関数x(X)をそれぞれ積分して、
$f(x) = \int X(x)\,dx\qquad F(X) = \int x(X)\,dX$
というふたつの関数f(x)とF(X)を考える。

まず、X(x)、x(X)が単調増加関数なので、f(x)、F(X)は下に凸な関数になる。
X(x)がx_*で不連続のときf(x)はx_*で微分できない。(左微分係数と右微分係数が異なる。) またX(x)が一定値を取る区間では、f(x)は微分係数(傾き)が一定だからその部分では一次関数と一致する。
X(x)、x(X)とその積分f(x)、F(X)の関係をまとめると次のようになる。

f(x)	X(x)	x(X)	F(X)
下凸関数	単調増加関数	単調増加関数	下凸関数
点x_*で微分できない。(左微分係数がX₁で右微分係数がX₂)	不連続点x_*で、左極限値X₁から右極限値X₂への不連続な増加。	X₁からX₂まで、一定値x_*を取る。	X₁からX₂まで、F(X)の微分係数が一定になる。
x₁からx₂まで、f(x)の微分係数が一定になる。	x₁からx₂まで、一定値X_*を取る。	不連続点X_*で、左極限値x₁から右極限値x₂への不連続な増加。	点X_*で微分できない。(左微分係数がx₁で右微分係数がx₂)

ここで、

f(x)とX(x)は、微分積分によって互いを再現することができる。(積分定数の不定性は除く)
X(x)とx(X)は、互いにほぼ逆関数で、不連続点での不定性を除けば互いを再現できる。
x(X)とF(X)は、微分積分によって互いを再現することができる。(積分定数の不定性は除く)

が成り立っているから、

f(x)とF(X)は、定数分の不定性を除いて、互いを正確に再現することができる。( X(x)とx(X)の不連続点での不定性は積分には効いてこないので、f(x)、F(X)の値には影響しない。)

下凸関数f(x)から下凸関数F(X)を得る

ここまでの話を踏まえると、下凸関数f(x)に対して次の手順をおこなうことで下凸関数F(X)が得られる。

f(x)は下凸関数なので、(1)連続関数になり、(2)ほとんどの点で微分可能になる。
f(x)を微分して、増加関数を得る。
- 微分不可能な点(X(x)は不連続な増加をする)での値は後の部分で効いてこないので特に決めなくていい。
増加関数X(x)の「ほぼ逆関数」x(X)を取る。(X(x)の不連続点はx(X)では一定値、X(x)の一定値はx(X)の不連続点とする。)
x(X)を積分して、 $F(X) =\int x(X)\,dx$ を得る。

逆に、この手順をF(X)に対しておこなえば、F(X)からf(x)を(定数の不定さを除いて)再現することができる。

関数f(x)に「微分不可能な点」も「微分係数が一定の区間」も無い場合は、x↔Xがちょうど一対一で対応するので、f(x)の値とF(X)の値も対応する。
「微分不可能な点」や「微分係数が一定の区間」がある場合は一対一では対応せず、

「f(x)の微分不可能な点」↔「xの1点にXの区間が対応」↔「F(X)の微分係数が一定の区間」
「f(x)の微分係数が一定の区間」↔「xの区間にXの1点が対応」↔「F(X)の微分不可能な点」

という対応関係になる。
一点と区間が対応しているので、一見すると変換の過程で必要な情報が足りなかったり削ってしまったりしそうだけど、微分係数一定の区間での関数値は区間の両端の値を直線的に結べば決まるので、問題なく変換が成立する。

この「下凸関数f(x) ↔ 下凸関数F(X)」の間の相互変換は、いわゆるルジャンドル変換と同じものになっている。

ルジャンドル変換

上でのf(x)からF(X)への変換を、普通のルジャンドル変換の形に近づけていく。

f(x)に微分不可能な点がなく微分係数が一定の区間もない場合

まず、f(x)に微分不可能な点がなくて、微分係数が一定になる区間もない場合を考える。
すると、部分積分により
$\begin{eqnarray} F(X) &= & \int^{X}_{X_0} x(X)\,dX = [X \cdot x(X)]^X_{X_0} - \int^x_{x_0}X(x)\,dx \\ &=& [X \cdot x(X)]^X_{X_0} - [f(x)]^x_{x_0} \\ &=& [X \cdot x(X) - f(x(X))]^X_{X_0} \\ &=& X \cdot x(X) - f(x(X)) +C \end{eqnarray}$

となり、定数項を消すと、通常のルジャンドル変換の式、

$F(X) = X \cdot x(X) - f(x(X))$

と一致する式が得られる。

f(x)に微分不可能な点がある場合

x=x_*でf(x)が微分不可能で、点x_*が区間[X₁, X₂]に対応しているとする。つまりx(X₁) = x(X₂) = x_*となっている。
この場合のF(X)を計算する。
XがX₁以下のときのF(X)は、さっきの計算と同じ。

X₂以上のXについてのF(X)を計算すると、
$\begin{eqnarray} F(X) &=& \int^{X_1}_{X_0} x(X)\,dX + \int^{X_2}_{X_1} x(X)\,dX + \int^{X}_{X_2} x(X)\,dX \\ &=& [X \cdot x(X) - f(x(X))]^{X_1}_{X_0} +(X_2-X_1)x_{*} + [X \cdot x(X) - f(x(X))]^{X}_{X_2} \\ &=& [X \cdot x(X) - f(x(X))]^X_{X_0} \\ &=& X \cdot x(X) - f(x(X)) +C \end{eqnarray}$
となり、微分不可能な点がない場合と同じ式が得られる。(x(X₁) = x(X₂) = x_*のため、式変形の途中で値が打ち消しあっている。)

X₁ < X < X₂となるXについて計算すると、

$\begin{eqnarray} F(X) &=& \int^{X_1}_{X_0} x(X)\,dX + \int^{X}_{X_1} x(X)\,dX \\ &=& X \cdot x_{*} - f(x_*) + C \end{eqnarray}$

となり、ルジャンドル変換の式で「x(X)」のところを x_* したものになっている。
また、この式は一次式になっているから、「f(x)が微分不可能になる点には、F(X)の微分係数が一定になる区間が対応する」と合致している。

f(x)に微分係数が一定の区間がある場合

今度は区間[x₁, x₂]でf(x)の微分係数が一定値X_*を取る場合のF(X)を計算する。

左からX_*に近づいた場合、x(X)→x₁となり、右からX_*に近づいた場合、x(X)→x₂となることに注意する。

X > X_*として、

$\begin{eqnarray} F(X) &=& \int^{X_*}_{X_0} x(X)\,dX + \int^{X}_{X_*} x(X)\,dX \\ &=& [X \cdot x(X) - f(x(X))]^{X_*}_{X_0} + [X \cdot x(X) - f(x(X))]^X_{X_*} \end{eqnarray}$

ここで、

第1項: $\Bigl(x_1 X_* - f(x_1) \Bigr) + C$
第2項: $\Bigl( X \cdot x(X) - f(x(X) \Bigr) - \Bigl( x_2 X_* - f(x_2) \Bigr)$

となる。
区間[x₁, x₂]でf(x)の微分係数は常にX_*なので、

$f(x_2) = f(x_1) + (x_2 - x_1)X_*$

が成り立っているので、第1項の前半と第2項の後半が打ち消しあって、ふたたび

$F(X) = X \cdot x(X) - f(x(X)) +C$

の式が得られた。

ルジャンドル変換の式

結局、f(x)に微分不可能な点や微分係数一定の区間がある場合も含めて

$F(X) = X \cdot x(X) - f(x(X)) \quad$ (Xは、f(x)の微分不可能点と対応しない)
$F(X) = X \cdot x_* - f(x_*)\quad$ (Xは、f(x)の微分不可能点x_*に対応する領域にある)

で、F(X)を計算できる。(定数C=0とした。)

この結果を図で見ると次のようになる。

関数 x(X) が右上象限に入る点を (X_s, x_s) = (X_s, x(X_s)) としておく。
このとき、図の右下の領域の面積と左上の領域の面積は、それぞれ

$\begin{array}{ccc} \int^X_{X_s}x(X)\,dX &=& F(X) - F(X_s) \\ \int^{x(X)}_{x_s} X(s)\,dx &=& f(x(X)) - f(x_s) \end{array}$

となる。これらの和が長方形の面積 x(X)・X になるので、

$F(X) = X \cdot x(X) - f(x(X)) + \Bigl(f(x_s) - F(X_s) \Bigr)$

が成り立ち、F(X_s) = f(x_s)となるようにF(X)を決めると

$F(X) = X \cdot x(X) - f(x(X))$

となる。ただし、f(x)の微分不可能な点や増加率一定の区間では、xとXが一対一に対応しないので、

f(x)の微分不可能な点(図のx_*)に対応する区間 [X₁, X₂] の間にXがある場合は、 $F(X) = X \cdot x_* - f(x_*)$ となる。
f(x)の増加率が一定の区間 [x₁, x₂] に対応する点 X_* の場合、この区間内のどのxの値を使っても、 $F(X) = X \cdot x - f(x)$ が成り立つ。

そして逆に

$f(x) = x \cdot X(x) - F(X(x)) \quad$ (xは、F(X)の微分不可能点と対応しない)
$f(x) = x \cdot X_* - F(X_*)\quad$ (xは、F(X)の微分不可能点X_*に対応する領域にある)

によってF(X)からf(x)を求めることができ、もとの関数が再現される。

熱力学の場合

熱力学では、関数f(x)のルジャンドル変換F(X)を $F = X \cdot x - f$ とせず、符号を逆にして

$F = f - X \cdot x$

の形で定義している。
このため、F(X)をXを微分すると(xにはならず) $\frac{F(X)}{dX} = -x$ となり、F(X)からf(x)への変換は

$f(x) = F(X(x)) + x\cdot X(x)$

となる。

熱力学では複数の変数についてルジャンドル変換をおこなうので、こちらの定義の方が考えやすい。

*1:凸関数でなくても定義はされるけど、逆変換しても元の関数に戻らない

2021-03-10

場の量子論への入門の一歩前

物理

目次:「1.場の量子論 = 粒子数の変化を扱える量子論」「2.生成・消滅演算子」「3.古典論への移行と量子化」「4.量子力学から場の量子論への移行」「5.量子力学から場の量子論への移行(古典場を経由しない仕方)」「6.終わり」

1. 場の量子論 = 粒子数の変化を扱える量子論

てっとり早く場の量子論を特徴づけると、

場の量子論 … 粒子数が固定されておらず、粒子の数の変化を扱える(粒子の生成・消滅を扱える)量子論。

のように説明できる。
それと対比させると「量子力学」は粒子数が固定されていて変化しない量子論ということなる。

(「量子力学」といったときに場の量子論も含める場合も多いけど、この文章では、場の量子論と対比させた意味で「量子力学」という言葉を使うことにする。)

ここで「粒子」と言っても、それは量子論的な「粒子」なので、粒子的な性質と波動的な性質の両方を合わせ持っており、日常で観察される何かの粒のように理解することはできない。それでも、

「生成」「消滅」ごとにエネルギーや運動量が離散的に増減し、「個数」(個数演算子)も定義できる。

という点で、粒子(何かのかたまり)のような性質を持っている。

また場の量子論では、日常的な感覚では粒子っぽくないものも粒子として扱うことができる。
例えば結晶格子の振動(音の波)を量子論を考慮して扱うと、離散的なエネルギー励起が現れる。このときのエネルギーの離散的な増減を、場の量子論では「粒子(フォノン)の生成・消滅」として扱える。

また粒子の性質だけでなく波動の性質も持っているので、「粒子の生成・消滅」を波動の視点から見ると「波の強さや周波数成分を離散的に変化させている」と表現することができる。

2. 生成・消滅演算子

粒子の生成・消滅を扱うために、運動量 ${\bf p}$ の粒子を生成する演算子 $\hat{a}^{\dagger}({\bf p})$ 、消滅させる演算子 $\hat{a}({\bf p})$ や、それらをフーリエ変換した $\hat{a}^{\dagger}({\bf x}),\hat{a}({\bf x})$ といった演算子が導入される。

こうした演算子の持つ性質が粒子の性質を規定するので、これらの演算子の性質を特定することが場の量子論の第一歩になる。(生成・消滅演算子が調和振動子の上昇・下降演算子と同じような性質を持っているので、場の量子論への導入として調和振動子の話から入ったりする。)

粒子の生成・消滅を扱うために導入された演算子は、空間の各点 ${\bf x}$ (またはフーリエ変換した運動量空間の各点 ${\bf p}$ )ごとに定義されているので場の演算子と呼ばれる。

3. 古典論への移行と量子化

場の演算子 $\hat{a}^{\dagger}({\bf x}),\hat{a}({\bf x})$ の適用によって状態が離散的に変化するけれど、この離散的変化があたかも連続的に見えるような近似(古典的極限)を考えると、粒子性と波動性のうち粒子的な性質が見えなくなり、量子論的ではなく古典的に扱える場の量 a(x) に移行する。*1
ただしこうして現れた場は、「古典的」とはいっても、その場を古典力学的・電磁気学的な現象として観察できるとは限らない。単に演算子などが登場せず古典力学的に取り扱えるという意味で「古典的」と言っているにすぎない。

逆に古典的な場から出発し、何らかの手続きによって場の量子論に移行する操作を「場の量子化」という。

また、古典場ではなく質点の力学から出発してそれを「量子化」すると量子力学に移行する。
これらをまとめると次の表のような関係になっている。

	有限自由度		無限自由度
古典論	質点		古典場
	古典極限↑　↓量子化		古典極限↑　↓量子化
量子論	量子力学 (粒子数固定)	← 粒子数固定	場の量子論 (粒子数可変)

場の量子論で、粒子の数が固定している場合(「個数」が保存量の場合)だけに状況を限定すると量子力学で扱える。
場の量子論で、粒子の生成・消滅による離散的変化が見えないくらい粒子数が多いと古典場として扱える(電磁場とか)。

このような話の脈絡だと「古典場を量子化して場の量子論を得る例」として、まずは電磁場が思い浮かぶ。
実際、歴史的にも光の輻射を量子論的に取り扱うための試行錯誤から場の量子論が生まれている。

ただし

マクスウェルの方程式自体が複雑なので、古典論の時点ですでに数式が面倒。
量子化するときゲージ自由度のことを考える必要がある。

というように、場の量子論一般に比べて扱いが面倒なので、場の量子論の本ではいきなり電磁場を扱うのではなく他の場を扱ったあとに回されることも多いみたい。*2

4. 量子力学から場の量子論への移行

量子力学が「粒子数固定の量子論」で、場の量子論が「粒子数の変化を扱える量子論」だった。
ということは場の量子論の方が扱う範囲が広いのだから、量子力学で扱っている問題を場の量子論の問題として扱うこともできるだろう。

量子力学と場の量子論には次のような関係があった。

	有限自由度		無限自由度
古典論	質点		古典場
	古典極限↑　↓量子化		古典極限↑　↓量子化
量子論	量子力学 (粒子数固定)	← 粒子数固定	場の量子論 (粒子数可変)

そこで、次のようにすれば量子力学から場の量子論へ移行できる。

何かちょうどいい古典場を取る。
その古典場を量子化する。
量子化して得た場の量子論の式が、もとの量子力学系と同じ結果を与えるようになっていればよい。

しかし、そのような「ちょうどいい古典場」は非常に混乱を生む性質を持っている。
それは、

粒子同士が相互作用しない場合、「ちょうどいい古典場」は、1粒子系の波動関数が満たす方程式と同じ方程式を満たす。(また場の演算子も同じ方程式を満たす。)

という性質。

波動関数は量子論的な概念で、その一方、古典場のほうは古典論的な概念(たとえその場が古典力学や電磁気学には登場しないような場だとしても)なので、そのどちらも同一の方程式を満たしてしまうというのは、両者の違いを曖昧にして混乱を生むことになる。
例えば、

質点の力学を出発点にして、それを量子化して波動関数の満たす方程式(シュレディンガー方程式とかクライン・ゴルドン方程式とか)を得る。
その方程式を満たしている古典場(これは波動関数とは別のもの)を考えて、その古典場を量子化して場の演算子を得る。

という手順で場の量子論に到達した場合、二回の量子化が関わっている。

ここで同一の方程式に従うふたつのもの(波動関数と古典場)があることを曖昧にすると、量子化して得たもの(波動関数)をもう一度量子化しているように誤解してしまう。*3

高橋康『古典場から量子場への道』だと3章でシュレディンガー方程式やクライン・ゴルドン方程式を導入し4章で場の量子化を扱っているけれど、読んでいて古典論の対象を扱っているのか量子論の対象を扱っているのか分からなくなって混乱した。

朝永振一郎『量子力学II』では、見かけは同一の方程式でも、波動関数が満たす式をSchrödinger方程式、古典場が満たす式をde Broglie方程式と呼んで区別している。

Schrödinger方程式とde Broglie方程式とが同じ形をとることから、量子力学の発見されたはじめのころは、この二つの方程式がまったく異なる概念に属するものであることが物理学者によくわからなかった。そこでこの差異に関する無知に基づいた混乱や無用の論争がしばしば起こったのであった。
(朝永振一郎『量子力学II』§50)

ディラックは彼の発見的方法に導かれて、Ψ(x)の満たすべき場の方程式がψ(x)の満たす方程式と同じ形をしていることを発見したのです。しかし方程式の形は同じでも、ψは1個の粒子の格率振幅で…Ψは波動場を記述する…というように、概念的にはまったく別ものであることを忘れてはいけません。
(朝永振一郎『スピンはめぐる』第6話)

また朝永『量子力学II』では、

「幾何光学と光の波動論」との類推から、電子の波動論としてde Broglie方程式を導く。(第6章)
- 量子現象を扱うとき「de Broglie方程式 + 量子化」を使っている。(6章§47)
マトリックス力学とde Broglie方程式との対応関係から、Schrödinger方程式を得る。(7章§49)

という説明をしている。つまり「古典場」から「量子力学」という説明の流れ。

5. 量子力学から場の量子論への移行(古典場を経由しない仕方)

前節では「波動関数と同一の方程式を満たす古典場を考えて、その量子化によって場の量子論にいたる」という流れで、量子力学から場の量子論への移行を説明した。
これとは別に、古典場は経由せずに、多粒子系の波動関数を生成演算子を用いた形に変形する、という説明の仕方もある。*4

同種粒子n個からなる系を量子力学で扱う場合、次のようにおこなわれる。

量子論では同種粒子は区別できないけれど、いったん区別できるかのように扱ってn個の粒子の座標をそれぞれx₁、…、x_nとして*5、n変数波動関数 φ(x₁、…、x_n) を考える。
その上で、n個の変数を入れ換えても同じ状態を表すような波動関数だけを選別して用いる。ボース粒子なら対称関数、フェルミ粒子なら反対称関数を取る。

場の量子論への移行は、このような対称関数や反対称関数で表されている系を生成演算子を用いた形に変形することでおこなう。

n粒子状態は、真空状態に生成演算子をn個適用したものとして表現される。
- 扱っている粒子がボース粒子なのかフェルミ粒子なのかというのは、生成演算子の持つ代数的性質によって表される。
生成演算子の適用を「状態1の粒子を生成する演算子の適用がN₁回、状態2の粒子を生成する演算子の適用がN₂回、…」のように表現すれば、各状態1,2,…のそれぞれにいくつの粒子が入っているかの占有数N₁、N₂、N₃、…によって系の状態を表していると見ることもできる。(占有数表示)

6. 終わり

ここまで来るとあとは数式を用いた話に入っていくことになるけれど、それは「入門の一歩前」ではなく「入門」の話になるだろう。

*1:「古典的極限」が正確にどういうことなのかよく理解できていないけれど、粒子の「数が非常に多く占有数を連続変数のように見なせる場合が古典的な極限にあたる」(サクライ『上級量子力学上』2.3節。3.10節も参照)と考えておく。cf. 首藤啓『古典と量子の間』(岩波講座物理の世界)。

*2:一方、量子力学の本で、本の終わり辺りで電磁場の量子化を扱っていることもある。物理入門コースの中嶋貞雄『量子力学II』がマクスウェル方程式に踏み込まず電磁波の式をあらかじめ与えた上で量子化を論じているので比較的読みやすい? 他に本の目次をながめてみると小出昭一郎『量子力学II』、猪木慶治・川合光『量子力学II』、砂川重信『量子力学』など。

*3:ただし歴史的に見ると当初は「一度量子化したものをもう一度量子化する」という道筋で場の量子化が導入されたみたい。「ここでディラックは、彼独特のアクロバットをやりました。…そもそもシュレーディンガー方程式はすでに量子化の結果あらわれたものです。…それを、第2量子化の名が示すように、もう一度量子化するということにいったいどんな意味があるのだろうか。凡人たちはここで戸惑いを感ぜざるを得ない。」(朝永振一郎『スピンはめぐる』第6話)、「最初これは「第2量子化」と見なされた。つまり、量子化される場は、電子のディラック波動関数のような、1粒子の量子力学で使われる波動関数だった。」ワインバーグ『場の量子論 1巻』1.2場の量子論の誕生)

*4:このアプローチが書かれている文献としては、一冊全体で80ページの新井朝雄『多体系と量子場』(岩波講座物理の世界) が分量的には最も手軽か? 他に北孝文『別冊数理科学統計力学から理解する超伝導理論』2章、高橋康『物性研究者のための場の量子論1』2章、小出昭一郎『量子力学II』11章、猪木慶治・川合光『量子力学II』11.3節、砂川重信『量子力学』6章§6など。

*5:各粒子が区別されアイデンティティを持ち消滅もしないため量子力学では座標演算子が考えられる。場の量子論では座標演算子は登場しない。場の量子論の観点からは、位置演算子の性質(交換関係)はどのように生じるのだろう?

2020-09-03

Rust入門を兼ねてプロジェクト・オイラーの問題を解く

プログラミング

とりあえず問100まで解くことに決めて始めたのだけど、問題の難易度やプログラムを書く面倒さが速いペースで増加していくので割と早い段階で問題を解くことが優先になって、Rustの機能やライブラリを理解することがおざなりになってしまった。
それでも言語の初歩的な部分についてはそれなりにRustの感覚が得られた気がする。

1. 整数とベクター

大部分の問題は、整数、整数のベクター、整数のベクターのベクター等々だけを使って解ける。
そのため、プログラムを書くときに所有権などのせいで書き方に困ることはあっても、そうした所有権とか生存期間とかの規則が問題を解く上で本質的な障害になることはそんなに無い。

「gotoしかない言語でプログラムを書いていた人がforやwhileだけでプログラムを書く」とか「破壊的変更が普通の言語を使っていた人がデータは基本的に不変な言語を使う」ような感じかも。
ベクターすら使う必要がなく整数を扱うだけで済む問題では、型の規則(不変可変、型の変換)にちょっとうるさいだけの普通の言語と思ってプログラムが書ける。

逆に、プロジェクト・オイラーの問題に取り組んでも、所有権や生存期間のことをよく考えないといけない場合についての理解はあまり深まらないとも言える。

よく使ったベクターの関数

push
- ベクターをあらかじめ大きなサイズを確保することはあまりなくてだんだん要素を追加していくことが多かったので、ベクターを使うときはだいたいpushを使っていた。
sort
- 重複するものを取り除く/重複しているかどうかの判定(dedupを併用)。
- ソートしたもの同士に対して同値性を比較する。
- 使わなくても済む場合(もっと計算が少なくて済む方法がある場合、ソートせずに操作しても結果は変わらない場合など)でも割と気にせず使っている。
- sort_by、sort_by_keyはあまり使っていなかった。
iter
- はじめのうちはあまりイテレーターを使わなかった(イテレーターの関数をあまり知らなかった)ので、途中からはsortよりも頻繁に使っている。
pop
- pushと比較すると使用する機会はだいぶ少ない。
dedup
- だいたい「sortしたあとdedupして重複を消す」という使い方。
  - 「各桁がすべて異なるか」みたいな条件の判定にも。
  - きちんと判定すれば同じ計算を繰り返すのを避けられる場合でも、判定をサボって最後にsort + dedupで重複を消すみたいな使い方も。
その他 (このあたりは、よく使ったというほとではない)
- remove、insert
  - 組み合わせなどを列挙、探索するときにremove、insertを組みで使っていることが多かった。
- append、reverse
  - 時々使っていたけど、ベクターでなくリストだったらもっと多用していたと思われる。
- swap_remove
  - 使う機会はほとんどなかったけど、cloneできないデータのベクターを使う機会が多かったら結構使っていそう。
- binary_search

2. イテレーター

ベクターへの操作をイテレーターの組み合わせて簡潔に書ける場合もある一方で、型や所有権に関するエラーが出て想定するように書けない場合もある。

たいていは型や所有権やライブラリ関数に対する理解不足が原因なので、動くように書き直していくことで型や所有権などへの理解が深まる。
エラーが消えないとかでどうにも困ったら(あるいは単に面倒になった場合も)添字でのアクセスに切り替えればよい。
- もともとプロジェクトオイラーの問題の傾向からしても、添字経由でベクターを操作する方が自然な書き方になる場合も多いので、イテレーターに無理に固執しなくても良い。
- 添字でのアクセスの方が所有権とか借用とかをあまり気にせず気楽に書ける。

よく使ったイテレーターの関数

rev
- forループで添字を降順で使いたい場合での使用が多い。
step_by
- ほとんど「step_by(2)」の形で使っていた。
map
- イテレーターの連鎖が分かりにくい感じになってmapを使うのをやめたことが何度かあった割には結構使っていた。
collect
- はじめのうちは結果を受け取る変数の型を指定して「let v: Vec<_> = 〜.collect()」みたいな書き方が多くて、だんだん「〜.collect::<Vec<_>>()」「〜.collect::<String>()」みたいに書くことが多くなっていた。どちらが見やすいのかはよく分からない。
fold
- 「ベクターの要素の和を取る」というのが一番多い使い方だった。sumがあるのに気づいてから使用する機会が減った。
zip
- zipをうまく使うと簡潔に書けることがある一方で、イテレーターの連鎖と参照がいろいろからんで分かりにくくなることも多い、という印象。
- rev(だったと思う)と組み合わせて使おうとしたときに型エラーをなくすのにしばらくかかった。
enumerate
- enumerateを使って書けそうな場合でも、単に添字に対してforループを回して添字でアクセスする書き方をすることが多かったように思う。
sum
- はじめのうちsumの存在に気が付かなかったので、初めから使っていたらもっと使っていたと思われる。sumの積バージョンproductは使える機会はあったはずだけど一度も使っていなかった。
max、min、max_by_key、min_by_key
- これも途中まで存在に気付かず、使える機会に使っていなかった。
その他 (よく使ったというほとではない)
- chain、find、all、any、peekable、cycleなどは別に使わなくてもいいなと思いながら使った気がする。

3. 標準ライブラリに無いもの

多倍長整数

多倍長整数(bignum)は標準には入っていないので、大きな数を扱わないといけない問題では何とかする必要がある。

多倍長整数が必要になるのは問100までのうち10問程度。(あと、64ビット整数だとオーバーフローするけど128ビット整数にするとオーバーフローしない問題が何問かあった。)
多倍長整数が要る問題のほとんどは、多倍長整数に対する足し算と掛け算の組み合わせで解ける。実装の効率を気にする必要も特にない。
多倍長整数の割り算まで必要な問題が1問あったけど、2で割る場合だけ実装するだけでも問題は解ける。(いくらか効率の悪い計算をすることになるけど。)
crates.ioにいくつか多倍長整数ライブラリが登録されているようなので、それを使った方が手っ取り早かったかも。

乱数

問100までのなかに、乱数が必要(乱数なしでも解けるけどたぶん行列計算が面倒)な問題が1問あるけど、乱数関数が標準では入っていない。

xorshiftは実装する手間があまりかからない。
crates.ioに乱数ライブラリがある。

4. テスト

Rustはコンパイル時に型のエラーをたくさん出すため、単純な間違いが早い段階で見つかる場合も多い。
一方で型エラーでは防げない単純ミスもたくさん存在する。数値や式の書き間違い、問題や仕様の捉え間違い、0番目から数えるか1番めから数えるかの間違い、「≦」と「＜」との間違い、真偽の扱いを逆にする、等々。
型システムで防げるミスをたくさん入れるような人間は型システムで防げないミスもたくさん引き起こすから結局テストが必要になる。

テストは近くに書けば書くほど書く心理的ハードルが下がる

Rustではテスト用のクラスやモジュールを定義せずにテストを書くことができる。テストを別ファイルに分けることもスタイルとして強制されない。

このとき、テストしたい関数の直下や直上にテストを書くようにすると気分的に非常に気軽にテストが書ける。テストを書こうとしたときにまず別クラス別ファイル別ディレクトリを作るみたいな余分なステップが必要ない。(別モジュール、別ファイルを作るにしても必要になってから分ければいい。)

また新しく書かれたばかりの関数やプライベートな関数は、関数名や引数や動作が頻繁に変わったり関数自体がなくなったり分解されたり統合されたりすることが多いけど、そうした変更にテストコードを追従させるのも、テストコードがテストされるコードのすぐ近くの方が楽にできる。要らなくなったテストの破棄も気楽にできる。
テストのメンテナンスコストが大きいからテストを書かない、みたいなことを避けられる。

Rustではテスト中の出力はデフォルトではキャプチャされるけど--nocaptureオプションをつけると出力されるから、出力を見て動作確認する(REPLで確認したりprintを埋め込んで確認する)ようなコードをまずテスト関数内に書いてテスト実行して確認して、次にそれをテストコードの形に直すということもできる。最初からテストの形で書いた方が楽な場合も多いけど。
また失敗しているテストの詳細を出力させてコードを直すなど、テストするコード/されるコードの連携がやりやすいという印象。

プライベートな関数に対するテストとパブリックな関数に対するテスト

プライベートな関数(メソッド)に対するテストを書けない(書く手間のかかる)言語やテスティングフレームワークと異なり、Rustではプライベートに対して何の手間もなくテストが書ける。

プライベートな関数の方が一般的に変更が激しいからそれに合わせてテストの変更も楽におこないたいのに、多くの言語のテスティングフレームワークではプライベートに対するテストを書くのが難しかったり抜け道的な手法を取る必要があって、テストを書くコストがむやみに高くなる。
テストコードが同じモジュール(または内部モジュール)に置かれるので、外部モジュール(外部クラス、外部ファイル)からプライベートな要素を覗いてテストしているという気持ち悪さ(モジュールシステムの意図・制約に逆らっている)を感じなくてよい。
- 概念的にはプライベートに対するテストは外部コードではなく内部コードの一部として見るべきなのだろう。
- 一方、パブリックなものになっていくほど外部から見た振る舞いや引数などが固定される傾向があり、それに合わせてテストも安定化し、公開されている振る舞いや契約を確認するものになりやすい。こうしてだんだん外部コード的なテストが増えていくことになる。(もちろん内部コード的なテストと外部コード的なテストをきっちり区別できるわけではなく、パブリックな関数であっても複雑なアルゴリズムを使っていたりすると振る舞いより内部ロジックの正しさをテストしたい場合もあるだろう。)

プロジェクト・オイラーでのテスト

もちろんプログラム一般と同じようにテストすればよいけど。

プロジェクト・オイラーでは、問題の中で小さい値での答えが与えられている場合がよくある。
例えば問1は(要約すると)「10未満の時の合計は23になる。では1000未満の時は?」と聞いていて、問4は「2桁の数を使った場合は9009が最大になる。では3桁では?」と聞いている。
こういう問題に対しては、問題文で答えが提示されている値に対して正しく答えているかどうかをテストにすることができる。問1なら解答を出す関数が引数10に対して23を返すかをテストする。
こうしたテストがパスしたからといって解答が正しいことは保証されないけど、いくらかの安心は得られる。
ただしこのテストが使えるのは、一般のnに対するプログラムを書ける場合に限る。例えば問4の場合、2桁と3桁のどちらの場合も解くプログラムを書くのは面倒なので、このテストは適用しにくい。

また問題文の中で数列や式などの値が具体的に例示されていることも多い。
問2ではフィボナッチ数列の初めの部分「1,2,3,5,8,13,21,34,55,89、…」が示され、問12では三角数「1,3,6,10,15,21,28,36,45,55,…」が示されている。(こうした例示がされているのは、問題の曖昧さを避ける意図もあるのだと思う。例えば数列の初項を何にするかとか0番から数えるか1番から数えるかなどの違いで答えが違った値になってしまう。問12では三角数の第7項目は28だと書くことで曖昧さを消している。)
こうした例示されている値をそのままテストに流用できる。もちろん自分で計算してテストを作ればいいのだけど、こうしたテストの正解(期待される値)の計算で間違えることもよくある。問題文に出ている値をそのまま使う方がいくらか信頼度があがる。

簡単な数式でも思った以上に何度となく入力ミスしていた(そしてだいたい型エラーはでない)けど、こうしたテストでよくミスが見つかった。
また間違えようがないからとこうしたテストを書くのをサボると、だいたいあとでもっと手間がかかることになった。プログラムのサイズが大きくないからそんなにひどいことにはならなかったけど。

2020-06-22

無職になる

本

2年前から給料未払いだったから実質無職だったのと変わらない気もするけど会社職場も消滅し正式に無職の状態になって3ヶ月ぐらいになった。貯金の残りからすると今年中にも破綻しそうだけど考えるのも面倒なのでとりあえず本を読んでいる。読んだ本のいくつか。

『今昔物語集二』(新日本古典文学大系)
- 去年手に取った本朝世俗部(新潮日本古典集成で読んだ)が意外と読み進められたので震旦部も読んでみた。いくらなんでも同じような展開の話が続きすぎるような。
『正史三国志英傑伝』
- 内容以前に人名地名が覚えられず読む端から頭から落ちていく。
- 漢文の載っている本は漢文に返り点が振ってあるものが多いけれど、徳間書店から出ている本の多くが原文、書き下し文、現代語訳の形で掲載されている。返り点なしで読めるかというとおおむね読めないのだけど。
- 漢文法や語法について書いてある本はすでに返り点の打ち終わった文を提示していて、なぜ他の仕方ではなくそのように解析されるのかの説明がない。『漢文解釈教室』みたいな本はないものか。
『プログラミングRust』
- 「これ何だったかな」と確認しようとするとだいたい索引に載っていなかった。索引より記憶の問題のようにも思える。
『英文読解講座』『越前敏弥の日本人なら必ず誤訳する英文』『英語リーディングの探究』『英文をいかに読むか』『実践英語のセンスを磨く』『英語の読み方、味わい方』
- 英文解釈系の本を続けて読んだけど、読めば読むほど、英語をまともに読めるようになるとは思えなくなっていく。
『枕草子』(新潮日本古典集成)
- 『枕草子のたくらみ』が非常に面白かったから読もうとは思っていたけどようやく。文章をおぼろげにしか読み取れない感じで読み進める。注に従来の解釈・説は間違いという指摘が多く出てくるけど、どのくらい妥当とされているのだろう。
『和泉式部日記』(新潮日本古典集成)
- とりあえず文字を追っただけで内容は紗がかかったように不鮮明。和歌の贈答が入ると不鮮明さが跳ね上がる。
『Murder in Mesopotamia』
- 邦訳は読んでいて核になる部分は覚えているし中東が舞台でイギリス生活に密着した単語があまり出てこないはずから読みやすいだろうという推測で選んでいた本。実際読みやすかったけど読むにつれてクリスティーの本の中でそんなに好きでなかったことを思い出した。
『The Tragedy of X』
- クリスティーに比べると分からない単語が多すぎて辞書を引くのをサボりまくり全体的にぼんやりとしか読めていない。そのせいなのかドルリー・レーンがすごく魅力のない探偵役に思えた。「マヌケな自称名探偵」とは言わないけど。
『Titan: The Fighiting Fantasy World』
- 邦訳を読んだ時期は上の2冊と同時期のはずなのに読んでいて懐かしさを感じる。読み終わってから邦訳が再刊されていたことを知る。
『短編ミステリの二百年』
- 1をようやく読んで、出たばかりの2も続けて読む。1巻は150ページ、2巻は250ページほどの評論がついていて、そちらがメインの読書になった。海外ミステリは読んでも好みから外れることが多くてこのアンソロジーも例外ではなかったけど、評論とのセットで満足度は高かった。
『ユリシーズIII』
- 読み残っていた14章太陽神の牛、15章キルケをようやく読んで一応全章を読み終わった。14章の「何が書いてあるか分からない」度がかなり高い。
- 柳瀬尚紀訳にも完結してほしかった。と思って確認したら柳瀬訳11章セイレーンが雑誌掲載されたのが2011年で時間感覚がおかしくなる。
『日本探偵小説全集11 名作集1』
- 北村薫による本の紹介や感想や評論はどれも面白いし編むアンソロジーも解説や対談は非常に面白い。のだけど選んでいる作品自体は好みでないものが多くて、多くのアンソロジーが読めていない。これも少しだけ読んでそのままにしていた。
- それより年刊日本SF傑作選が2013年度(さよならの儀式)以降の全部を積み残しているのだった。こちらは次が出るのを楽しみにしていたはずが読み終わる前に次の巻が出て読むのが止まってしまった。
『平家物語』(講談社学術文庫)
- 出たときに買って分量の多さにそのままにしていた。原文のあとに現代語訳、語釈、解説が付いていて読み進めやすい。その代わり文庫で700ページ×4冊で読んでも読んでも終わらないのはつらかった。
『宇治拾遺物語』(講談社学術文庫)
- こちらは800ページ×上下巻だけど、平家物語よりサクサク読めた印象。『今昔物語集』と比べて話の扱い方や語り方の感じは好みのような気がする。
『古今和歌集』(新潮日本古典集成)
- 物語や説話や日記に和歌が出てくるとだいたい何を言っているのか分からないことが多いのだけど、それと比較すると意外なほど内容を読み取れる歌が多い。物語等に出てくる和歌は状況文脈を踏まえて込められた意味を読み取らないといけないから理解の難易度が高くなっていたのかも。