トップ > 数学 > p進展開について

p進展開について

数学 整数論

ネイピアや小数の話からの派生で、p進展開についてのメモ。

整数間の距離

日常の感覚だと、0に一番近い正整数は1で、次に近いのは2、次が3、4、5、6、……とだんだん0から離れていく。
でも、それとは違う距離感覚を与えることができる。
まず任意に正整数pを取る。pは本当は素数にするのが都合がいいのだけど、都合が悪くなるまでは素数に限定しない。そして、pで割ったときの余りが等しい数同士は、等しくない数とよりも距離が近いと考える。pで割った余りに注目して、同じ余りのものは似ている→より近い、という感覚。
例えばp=3としたとき、次のようにグループを分ける。

  • グループ0: ……, -9,-6,-3,0,3,6, 9…… (3で割ったときの余り 0)
  • グループ1: ……, -8,-5,-2,1,4,7,10…… (3で割ったときの余り 1)
  • グループ2: ……, -7,-4,-1,2,5,8,11…… (3で割ったときの余り 2)

このとき同じグループに入っている数の間の距離は、違うグループ間の距離よりも近い。

さらにpで割ったときの余りが同じだけでなく、p2で割った余りが等しい場合、距離がもっと近いと考える。p=3の場合は次のよう分類できて、同じサブグループに入っているとより近い。

  • グループ0: (3で割った余り 0)
    • グループ00: -18,-9,0, 9,18,27 (9で割った余り 0)
    • グループ10: -15,-6,3,12,21,30 (9で割った余り 3)
    • グループ20: -12,-3,6,15,24,33 (9で割った余り 6)
  • グループ1: (3で割った余り 1)
    • グループ01: -17,-8,1,10,19,28 (9で割った余り 1)
    • グループ11: -14,-5,4,13,22,31 (9で割った余り 4)
    • グループ21: -11,-2,7,16,25,34 (9で割った余り 7)
  • グループ2: (3で割った余り 2)
    • グループ02: -16,-7,2,11,20,29 (9で割った余り 2)
    • グループ12: -13,-4,5,14,23,32 (9で割った余り 5)
    • グループ22: -10,-1,8,17,26,35 (9で割った余り 8)

当然次が考えられて、p3で割った余りも近い場合はもっと近いとする。さらに同様にして、p4で割った余り、p5で割った余り、……というように、より大きなkについてのpkで割ったときの余りが等しい場合に距離が近いと考える。
このように考えた距離は日常使う距離とは全く違うのだけど、これを判りやすく見る方法がある。

自然数のp進展開

上で与えた距離で考えた場合、二つの数がどれくらい近いのかはすぐには判定できないように思える。
でもp=10の場合に限ればすぐに距離が判定できる。例えば次の三つの数を考える。

  • 31402、31404、731402

31402と731402は下5桁が等しいので、p=10、p2=100、p3=1000、p4=10000、p5=100000、で割った時の余りがどれも等しくなる。したがって31402と731402との距離は他の多くの数とよりもかなり近いことが判る。一方、31404は下1桁目が他の二つの数と違うのでp=10で割った余りがすでに異なるため、他の二つの数との距離は近くない。このように下の桁から見ていって等しい桁が多ければ多いほどp=10での距離が近いことがすぐに判断できる。
同様の判定法はp=10以外の場合にも使うことができる。数をpを基底としたp進展開した形で表示してやればいい。例えば、1から9までを3進で表示すると次のようになる。

10進表示 3進表示
0 0000
1 0001
2 0002
3 0010
4 0011
5 0012
6 0020
7 0021
8 0022
9 0100

これを見ると下2桁まで一致しているのは0と9だけなので、この二つの数は他の数と比べてp=3での距離が近いと判断できる。

p進距離、p進絶対値

ここまで「より近い」みたいな曖昧な言い方をしてきたけど、距離に具体的な数値を与えることにする。また、ある数aの絶対値はaと0との距離なので、絶対値も同時に与えたことになる。
aとbとの「p進距離」を次のように定義する。a-b= pkl (ただしlとpは互いに素)のときaとbのp進距離は1/pk(これは、aとbをそれぞれp進展開したときに下k桁まで一致しているときの距離は1/pk、と言ってもいい)。
こう定義したp進距離は、日常的に使っている距離と比べておおよそ逆になっている。なぜなら通常の距離の場合、小数点以下k桁まで一致している場合、距離は1/10k未満になるので。次の二つの数
12345.678912……
12345.678987……
は小数点以下4桁まで等しいの、両者の距離は1/104未満。
一方、(p=10として)p進展開表示されている次の二つの自然数
35467
54467
は下3桁が等しいのでp進距離は1/103になる。
aの絶対値は、aと0との距離なので、p進展開したときに下k桁が0となる場合、p進絶対は1/pkとなる。
通常の絶対値の場合、桁を左にひとつシフトすると絶対値が10倍になり、右にシフトすると絶対値は10分の1になる。一方、p進絶対値の場合(p進展開表示したものを)左にシフトすると1/p倍で右にシフトするとp倍になり、通常の絶対値と逆の関係になっている。
したがって通常の絶対値では、次の数列がどんどん0に近づいていく。

123
 12.3
  1.23
  0.123
  0.0123
  0.00123
……

一方、p進絶対値で考えると、次の数列がどんどん0に近づいていく。

    123
   1230
  12300
 123000
1230000
   ……

負の整数のp進展開

負数の場合、符号付きのp進展開表記ではp進距離が判りにくい。
たとえばp=10として、-3527と3527を考える。これらは下4桁が一致している。でもこの二つの数は、10を割った余りが等しくない(当然、102、103、104で割った余りも等しくない)。つまり-3527と3527は表記上は似ているのに、距離的には全然近くない。
-3527にp進的に近い正整数を探すと、例えば105-3527が考えられる。あるいは106-3527の方がもっと近い。10k-3527でkが大きくなるほど、-3527に近い数になる。
105-3527 = 6473
106-3527 = 96473
107-3527 = 996473
108-3527 = 9996473
109-3527 = 99996473
この10k-aというのは、いわゆる10の補数(基数の補数)。
補数の桁kを増やせば増やすほど、距離1/pkはどんどん0に近づいていく。そこで、無限桁を使った補数表現で負数を表すことにする。そう決めた。
-3527 = ……99999996473
正の数の列、6473、96473、996473、9996473、99996473、……が負の数-3527にだんだん近づいていくというのは気持ち悪い、変だと感じるかもしれない。でもそれは通常の距離感に引きずられている。通常の距離では正数と負数は0をはさんで互いに遠くにあるけれど、p進距離では負数の近くには正数も負数もどちらもたくさんある。p進距離で考える場合、数直線的なイメージは捨てるべき。

もっと一般的に、p進表現の桁を一桁ずつ順番に増やしていったとき、そのp進表現が表している数がある数cにどんどん近づいていく(距離が0に近づいていく)なら、無限桁の表現で数cを表すことに決める。ただしこの無限桁表示は、あくまで近づいていく相手cが存在している場合に限って数を表すだけで、近づいていく相手がない表現はどんな数も表さない。ここまでの段階(整数の範囲)では補数表現(ある桁より先の桁は全てp-1)の場合しか意味を持たない。
例えば、1、11、111、1111、11111、111111、……という数列に対して距離がどんどん縮まっていくような整数は存在しないので(整数の範囲で考える限り)「……111111111」という表現は何も表していない。

こうした無限桁表現の扱いは、通常使っている小数展開とおおむね類似している。通常の小数表現の場合、
小数の桁をどんどん増やしていったとき、それがある数cにどんどん近づいていく(距離が0に近づいていく)なら、無限桁の小数表記は数cを表す。
これを受け入れるなら、「1=0.9999……」は当然受け入れないといけなくなる(0.9、0.99、0.999、0.9999、……と1との距離は0に近づいていくので)。「1=0.9999……」を認めたくないというのは、無限小数表記が何を表すかについて上の説明と異なる内容を持ち込んでいることになる。(あと「1=0.9999……」の話でよく実数の性質(完備性)を持ち出した説明がされるけど、実数の性質はこの話に不要。有理数の範囲でも「1=0.9999……」は定義上成り立たないといけない)。
(実際にはこういう話だけでは「1=0.9999……」の疑問は解決しないので面倒だったりする。そもそも、無限小数表記によって何を表しているのかをちゃんと説明された記憶がない。なのに「ある数にどんどん近づいていくなら云々」という話を後出しされても、納得しない人は納得しないだろう。無限小数が何を表しているのかについてちゃんとした説明もされていないのに、あの表現で何かの数を表していることをたいていの人がどうして納得しているのかについての視点が抜け落ちている。小数展開アルゴリズム=筆算を実際に試すことで分数が無限小数に置き換わることを習得したというのが理由の一つかもしれない。そうすると、展開アルゴリズムを普通に適用した場合には出てこない0.9999……をうまく受け入れられなかったり不審に感じたりするというのはあるかもしれない。けれど脱線なので以下略)。

p進展開のアルゴリズム

上のような説明だけだと、「……9999999」と-1、「……9996473」と-3527がそれぞれ等しいことは確認できるけど、負数が与えられたときにそこからp進展開表現をどうやって求めればいいかは説明されていない。ひとつには、符号を正に変えたもののp進展開を求めてからそのpの補数を取る(各桁を反転させてから1を足す)というやり方があるけど、そうしないでも正数の展開と同じやり方をそのまま実行すれば負数についても展開が得られる。
つまり負数c0をp進展開表記にしたいなら
c0 = a0 + p c1 (0≦a0<p)
c1 = a1 + p c2 (0≦a1<p)
c2 = a2 + p c3 (0≦a2<p)
……
を満たすa0、a1、a2、……を計算すれば、「……a2a1a0」がp進展開表現になる。
例えば-3527の場合
-3527 = 3 + 10×(-353)
-353 = 7 + 10×(-36)
-36 = 4 + 10×(-4)
-4 = 6 + 10×(-1)
-1 = 9 + 10×(-1)
-1 = 9 + 10×(-1)
……
となるので、「……996473」と表示できることになる。

有理数の場合

ここまで考えてきたp進距離やp進展開表記を有理数に拡張してやりたい。ただし以下ではpは素数とする。
有理数aをpで割った余りというのは、aをa=b + p×c (bは0≦bkl/m (ただしlとp、mとpはそれぞれ互いに素)となるとき、aとbのp進距離は1/pkと定義する。この定義は整数のときの拡張になっている。

次に有理数のp進展開を考える。分母にpの巾しか現れない場合は簡単。p倍すると左に一桁シフトされpで割ると右に一桁シフトされるので、1/pのp進展開は0.1とすればいい。
例えばp=3として、次のようなp進展開が得られる。

数 p進展開(p=3)
63 (= 7p2) 2100
21 (= 7p) 210
7 21
7/3 (= 7/p) 2.1
7/9 (= 7/p2) 0.21

次に分母にpを含んでいない有理数のp進展開を考える。これは整数のp進展開と全く同じアルゴリズムを適用してやればよい。
有理数c0に対して
c0 = a0 + p c1 (0≦a0<p)
c1 = a1 + p c2 (0≦a1<p)
c2 = a2 + p c3 (0≦a2<p)
……
となるa0、a1、a2、……を求めていく。ただしa0、a1、a2は自然数で、c0、c1、c2は有理数とする。これを満たす自然数a0、a1、a2は必ず存在する(pが素数でない場合は存在するとは限らない)。こうやって……a2a1a0を作っていくと、だんだんc0に近づいていく数列が構築される。たとえばp=3のとき
1/4 = 1 + 3×(-1/4)
-1/4 = 2 + 3×(-3/4)
-3/4 = 0 + 3×(-1/4)
-1/4 = 2 + 3×(-3/4)
-3/4 = 0 + 3×(-1/4)
……
となるので、1/4は「……20202021」とp進展開表記される。
分数の値がこんな風に表記されるのは直感とかけ離れていて不自然だという感覚はたぶん正しい。日常とは違った距離感を考えて、その距離に都合のいい表記をおこなっているので。しかも、分数には実数を近似するという役割があるけど(例えば22/7でπを近似するとか)、p進距離には実数の近似という役割は持っていないのでさらに直感とずれている。
それでも4(p進表記では「11」)と「……20202021」とを筆算で掛け算してみると「……00001」となるので、つじつまはあっている。
また整数の時と同様に、2数間の距離はp進展開した表示の下の桁がどこまで一致しているかを見れば判る。たとえば5(p進表記「12」)と2/9(p進表記「0.02」)は小数点右2桁目で違っているので距離は32と判断できる。実際5-2/9=43/32となっている。

あと、通常の10進表記の場合に筆算で割り算をするのと同じ要領で、分数のp進展開表記を筆算で求めることができる。ただし、下の桁から計算していく、引き算した結果に負数が現れる場合があるけどその場合は補数で表記する、といった違いがある。
例えば1/5は「……1210121012102」とp進展開されるけど、これは筆算で次のように求めていける。
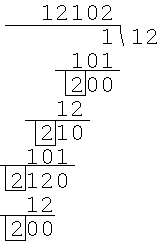(計算途中の様子。四角で囲ってあるのは補数になっている=左側に2が続いていることを示している。くわしい説明は略す)
分数のp進展開は必ず循環するし、逆に循環する無限桁表現は何らかの有理数を表現している。そのため、循環しない無限桁p進表現はどんな有理数も表さない無意味な表現ということになる。
有理数を通常の10進表記で表した場合とp進表記で表した場合を比較すると、次のようになる。

小数点の左側 小数点の右側
通常の10進表記 有限桁 有限桁 or 循環する
p進表記 有限桁 or 循環する 有限桁

p進数体

今までの話は、通常とは違う距離を導入してその距離と相性のよい新奇な表記を導入しただけで、扱っているもの自体は有理数にすぎない。でもそこから踏み出すこともできる。
有理数をp進表記すると、小数点の左側は有限桁になるかどこかから循環するようなものしか現れない。ここで循環しない表現も何らかの数を表していると考えてみる。
通常の10進表記では、小数点の右側に循環しない小数表現が出てくると、それは有理数ではない実数を表す。有理数と実数の関係は「有理数たちが(通常の距離にしたがて)並んでいて、その隙間を新たな数で埋めてやると実数が得られる」と説明される。
それと同様にp進表記の場合でも、小数点の左側に循環しない無限桁の表現が出てきても、それも何かの数を表しているように数の範囲を拡張することができる。この状況は「有理数たちが(p進距離にしたがって)互いに距離を取って集まっていて、その隙間を新たな数で埋める」と説明できる。そうして得られるのがp進数体Qpと呼ばれる何か。


追記: 関連→メモ: ヘンゼルの補題