ドラクエと類体論 - 再帰の反復blog

ドラクエ世界の形
パラレルワールドと被覆
被覆変換と被覆空間の住人たち
被覆のガロア対応
体のガロア理論
普遍被覆と基本群
文献
ヒルベルトの類体論

ドラクエ世界の形
パラレルワールドと被覆
被覆変換と被覆空間の住人たち
被覆のガロア対応
体のガロア理論
普遍被覆と基本群
文献
ヒルベルトの類体論

ドラクエ世界の形

ドラクエ(に限らず色々なコンピュータゲーム)に関する定番の疑問(ツッコミ)のひとつに「あの世界はいったいどんな形をしているのか」というのがある。ドラクエやそのほか多くのゲームの世界では正方形の世界の北と南、東と西がつながっている。

しかし地球のような球形の世界はこのようにはなっていない。
おそらくこの疑問に対する標準の答えは
「あれは球形の世界ではなくドーナツ形(トーラス)だ」
というものだろう。
またそれと同じくらいありそうな答え方は「あの世界は球面ではなく真っ平らで、世界地図で見た北と南、東と西が(ちょうど巨大などこでもドアが置いてあるかのように)繋がっている」というもの。プログラムの処理的にはこれが「正解」だろう(もちろんゲーム世界の設定とプログラムのやっている処理を同一視する必要は別にないけれど)。単なる解釈のひとつではなく実際にこれが正しい設定になっているものもある(例えば『真ウィザードリィRPG』、イーガン「ボーダー・ガード」)。
しかしこれ以外にも可能な答えがある。
「実は、世界地図に描かれている世界とそっくりな世界がたくさん存在していて、それらが平面上にタイルのように無限に並んでいる。各領域ごとに全く同じ姿をして全く同じ行動する人々がいて、もちろん主人公とそっくりな人も各領域ごとにいてそれぞれ同じ行動をしている。だから東に進んでいくと西から戻ってくるのではなく、東隣りにあるそっくりな領域に移動している。代わりに西の領域にいた主人公が自分がもといた領域にやってくるのだ」
この答え方は前二つの答えに比べるとマイナーだけど、といって特別珍しい考えでもないはず。
さらに別の回答もある。それは

そっくりな世界がたくさん存在している。
東西、南北がどこでもドアのように繋がっている。

の両方の解釈を組み合わせる。
まずそっくりな世界がいくつか存在していて、それらが縦横に並んで板チョコのような長方形の領域を形成している。そしてその長方形の領域の東と西、北と南が繋がっている、と考える。

縦に並ぶ世界の数と横に並ぶ世界の数を変えるごとに世界の形は違ったものになる。だから世界の形としてありえるものは無限にあることになる(それらのなかには、南北方向では繋がっていて東西方向はそっくりな世界が無限に並んでいるパターンや、東西南北全方向に無限に並んでいるパターンも含まれる)。

パラレルワールドと被覆

世界の形状には無限の可能性がある。しかしどれか一つだけを選ぶ必要は無くて、あらゆる形状の世界がパラレルワールドのように存在していると考えればいい。ただし普通のパラレルワールドでは世界ごとに人々の行動や状況が異なっているのに対して、ここで考えているパラレルワールドでは全ての世界(の、全ての領域)で状況も人々の行動もまったく同じになっている。
また平行世界のそれぞれが単に別々に存在しているだけでなく、それらの世界の間に階層関係的な秩序が存在している。
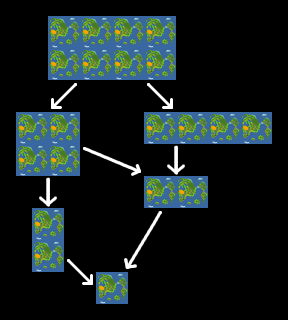
例として縦2×横4の世界を取る。
この縦2×横4の世界の各点・各人物に対して、縦1×横1の世界(普通の世界)における同一点・同一人物を対応させる。すると、この対応関係は2×4世界の八つの点を1×1世界の同一の点に対応させるような連続写像(=もとの世界で互いに近い点は行った先でも互いに近くなるような対応関係)になる。

このような関係を(不分岐な)被覆といい、縦1×横1の世界は底空間、縦2×横4の世界は被覆空間と呼ばれる。また底空間の同一の点に移されている点は互いに共役であるという。縦2×横4の世界では各点が自分自身も含めて八つの共役を持っている。
しかし縦2×横4の世界は縦1×横4の世界を二つコピーして繋げた世界と見ることもできる。よって縦2×横4の世界と縦1×横4の世界の間にも被覆関係を考えられる。このように考えた場合は、各点は二つの共役を持つことになる。

また縦1×横4世界も縦1×横1世界の被覆空間になる。縦2×横4世界を写像の出発点にすると次のような被覆関係がある。

このようにたくさんあるパラレルワールドの間には被覆関係という秩序が存在する。特に東西南北全方向にそっくりの領域が果てしなく続いて決して反対側から戻ってくることのない世界が一番大きな空間で、その他すべての世界に対する被覆空間になる(これは普遍被覆と呼ばれるものであとで再び登場する)。

被覆変換と被覆空間の住人たち

様々なパラレルワールド存在する人々はそれぞれ全く同一の行動を取っている。
どうして全く同じ行動になるかについての一つの考え方は、それぞれの世界に住んでいる人々が全く同じ状況で全く同じものを見聞きして全く同じように考えるので全く同じ行動になる、というもの。

別の考えとしては、住んでいる人々が全員が何者かに操られているというもの。一人一人は自由に動けないことに絶望していたり何も考えなくていいから楽だとか色々考えているけれど、そんなことには全く関係なく全ての世界の全ての領域で対応する人々は皆同じ行動をする。ここではこちらの考え方をとる。

あらゆる世界の全ての人々は定められた同一の行動しか取ることができない。しかし行動の自由が完全に失われているわけではなく、ほんの少しだけ逸脱する魔法が存在する。
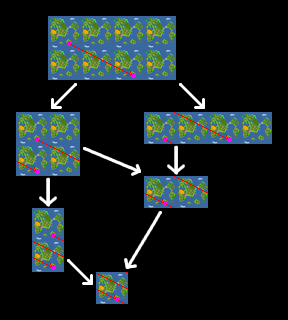
例えば縦2×横4の世界には八つの共役点が存在した。ここで、ある点にいる人がその点の共役点のどれかにテレポートしたと考えてみる。この時、各共役点にいる人達(その人とそっくりで全く同じ行動をとる人達)も同時にうまくテレポートさせれば同一点でぶつかることはない。彼らはパラレルワールド全体の行動からは少しだけ逸脱したことをしているけれど、全くそっくりな場所に移動するだけなので全体のつじつまは合っている。
ただしこの魔法のつじつまをちゃんと合わせるにはもう少し詳しく考える必要がある。
まず、魔法を使ったとき遠く離れた全ての共役点についても魔法が発動しなければならない。これはすでに述べた。
またもしも他の誰かと手を繋いでいるとしたら、その人もいっしょに跳躍した方が良いだろう。もちろん他の人は動かないと考えることもできるけど、そのように考え出すと同一人物の体の半分だけが移動するみたいな嫌な考えもできてしまうので、それは避ける。逆に、手を繋いでいるかどうかは無関係に近くにいた人は魔法を使ったあとも近くに移っているということにする。そうすれば互いに近くにいる同一パーティの人々は同じ場所に移動することになる。

さらにもっと遠く離れている人同士が同じロープの両端を持っている状態で魔法を使ったとする。その場合、魔法を使った後も互いに同じロープの両端を持った位置にいるだろう。そして手を繋いでいるかどうかに関係なく互いに近くにいた人が近い場所に飛ぶのと同じ理屈で、二人がたとえロープを持っていなくても魔法を使う前と使う後で二人の相対的な位置関係は変わらないことになる。
つまりこの魔法を使ったとき、世界の全ての人々に対して一斉に魔法が発動して、近くにいる人同士は互いに近くに移動し全体の相対的な位置関係は変化しない(これは被覆空間から自分自身への連続写像であるということで、このような魔法は数学的には被覆変換と呼ばれるもの)。このように条件をつけると、ある点からどの共役点に移動するかを決めるとその他の全ての点でその移動先が自動的に決まる。例えばある点が南に1東に2進んだ先の共役点に跳んだとすると、どの点も南に1東に2進んだ共役点に跳ぶことになる。

ただし、どの共役点についても必ずそこに飛ぶ魔法が存在するとは限らない。世界の形状によっては近くにいる人同士は必ず近くに移動するという条件を満たせずつじつまが合わなくなる状況もあって、その場合は魔法は発動しない(そのような例はあとであげる)。
ここで考えている状況(トーラスの被覆面)ではどの共役点をとってもつじつまが合うので共役点の数=魔法の種類になり、縦2×横4の世界では八つの魔法(被覆変換)が存在する。南にi、東にj跳ぶ魔法を(i,j)と書くことにすれば、
(0,0), (0,1), (0,2), (0,3)
(1,0), (1,1), (1,2), (1,3)
の八つになる。またこれらの魔法は合成(足し算)することもできる。(0,2)+(1,1)=(1,3)とか(1,2)+(1,2)=(0,0)とか。

被覆のガロア対応

さらに魔法を拡張して、被覆変換の魔法を使ったときに被覆写像を通して他の世界の人々も跳ばせるようにしてみる。
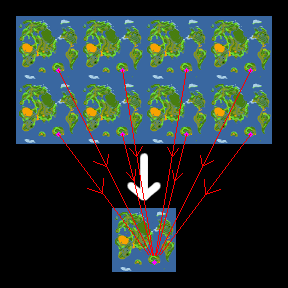
例えば縦2×横4の世界で(1,2)魔法を使うと、他の世界では次のように魔法が発動する(ある一点についての移動だけを図示している)。

このとき、縦1×横2世界と縦1×横1世界では魔法の発動前と発動後で位置が変わっていない。特に縦1×横1の世界では共役点がひとつしかないので、どの魔法を使っても位置が変化することはない。
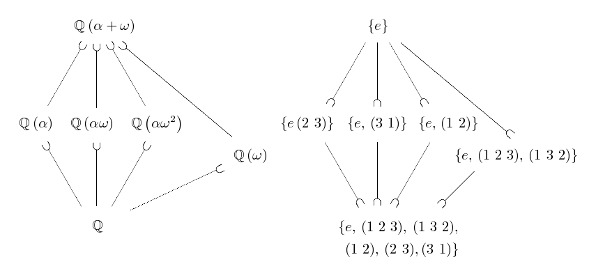
各世界について、どの魔法で位置が変化しないかをまとめると次の表のようになる。ここで右辺の各行は一番下の行(全ての魔法からなる群)の部分群になっていて、しかも全ての部分群が現れている。

世界	変化のない魔法
縦2×横4	(0,0)
2×2	(0,0), (0,2)
1×4	(0,0), (1,0)
2×1	(0,0), (0,1), (0,2), (0,3)
1×2	(0,0), (0,2), (1,0), (1,2)
1×1	(0,0), (0,1), (0,2), (0,3), (1,0), (1,1), (1,2), (1,3)

逆に縦2×横4の世界で右辺の魔法を使って移動できる点を全て同一視してやると左辺の世界が得られる。
このように、世界とその世界を変化させない魔法の集合には対応関係があり、世界の被覆関係が集合の包括関係に移される。これを図示すると次のようになる( $\subset$ に線の付いた記号は $\subset$ と同じ意味)。

この被覆と被覆変換群の対応は被覆空間のガロア対応と呼ばれる(たぶん普通はこれにさらに普遍被覆と基本群の話まで含めてそう呼ぶ)。ここでは縦2×横4の世界を例に使ったけれど、縦横の領域の数をいくつで考えても同様の対応が成り立つ。なので、その世界の全ての魔法からなる集合(これは群になる)を作ってその群にどんな部分群があるかを調べれば、中間にどんな空間があってどんな被覆関係になっているかを把握することができる。
ただしこの対応はどんな被覆を考えたときでも成り立つわけではない。先に「各共役点について必ずそこに飛ぶ魔法が存在するとは限らない」と書いたけれど、どの共役点に対してもそこに跳ぶ魔法(被覆変換)が存在する場合をガロア被覆とか正規被覆と呼び、ガロア被覆の場合にガロア対応が成り立つ(共役が有限個の場合は、「共役の個数=被覆変換の個数」というのがこの対応が成り立つ鍵)。

ガロア被覆でない例

次のような場所があるとする。通路の上と下がそれぞれループしている。

これを底空間として次のような被覆空間を考える。

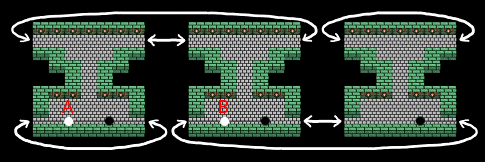
被覆空間なので各領域の同じ位置には同一人物がいる。
ここで点Aから共役点Bに跳ぼうとしてみる。点Aにいる人(白丸)は近くにいる人(黒丸)と二本のロープ(赤色の線)で繋がっている。もしも点Aから点Bに跳んだとすると、黒丸の人の跳躍先は二つのロープのどちらをたどるかによって違った位置になってしまう。跳ぶ先のつじつまが合わなくなるので、点Aから点Bに跳ぶ魔法は発動しない。同様に、残るもうひとつの共役点にも跳ぶことはできない(その確認は省略)。そのため可能な魔法はもとの位置から動かないものだけになる。
よってこの被覆はガロア被覆ではないのでガロア対応は存在しない。
ただしもう少し世界を広く取ると次のようなガロア被覆が得られる。同じ形の世界に対して被覆写像の対応のさせ方が三つある。

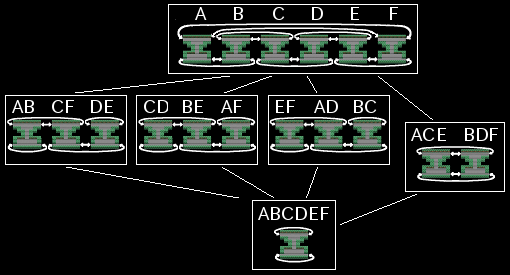
被覆変換は領域Aをどこに移すかで決まるのでそれを「A→B」のように書くと、ガロア対応の被覆変換側は次のようになっている。

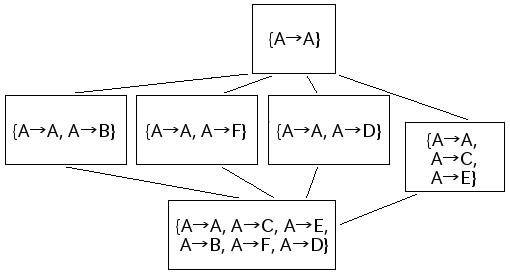
体のガロア理論

ここまでの話とよく似たことが体のガロア理論(普通のガロア理論)でも成り立っている(歴史的な登場順では体のガロア理論が先になるけど)。

被覆	体
底空間	基礎体
被覆空間	拡大体
被覆変換 (位置の置換)	体の自己同型写像 (根の置換)
被覆変換群	自己同型群
ガロア被覆共役の数=被覆変換の個数	ガロア拡大拡大次数=自己同型写像の個数
ガロア対応中間被覆 $\leftrightarrow$ 部分群ガロア被覆である中間被覆 $\leftrightarrow$ 正規部分群	ガロア対応中間体 $\leftrightarrow$ 部分群ガロア拡大である中間体 $\leftrightarrow$ 正規部分群

例: $\mathbb{Q}(\sqrt{-2})$

体のガロア理論については詳しく説明しないけれど、例として有理数 $\mathbb{Q}$ に $\sqrt{-2}$ を付け加えてできる体
$\mathbb{Q}(\sqrt{-2})= \left\{a+b\sqrt{-2} \middle| a,b \in \mathbb{Q} \right\}$
を考える。このとき $\sqrt{-2}$ の(有理数体 $\mathbb{Q}$ 上の)共役は、 $\sqrt{-2}$ 自身と $-\sqrt{-2}$ の二つ(どちらも $x^2+2=0$ の解)。
ガロア拡大になるための条件は「拡大次数=自己同型写像の個数」で、(この文脈では)「拡大次数=添付した元の共役の個数」が成り立つので、 $\sqrt{-2}$ の各共役ごとに自己同型写像が存在すればガロア拡大になる(もう少しだけ詳しいことは「方程式からガロア理論」)。
$\sqrt{-2}$ を、 $\sqrt{-2}$ または $-\sqrt{-2}$ に置き換えると、それに伴って $\mathbb{Q}(\sqrt{-2})$ 上の自己同型写像が二つ(恒等写像と複素共役写像)生じるので、 $\mathbb{Q}(\sqrt{-2})$ は $\mathbb{Q}$ のガロア拡大。

根の置換	自己同型写像
$\sqrt{-2} \mapsto \sqrt{-2}$	$a+b\sqrt{-2} \mapsto a+b\sqrt{-2}\;$ (恒等写像 ${\rm id}$ )
$\sqrt{-2} \mapsto -\sqrt{-2}$	$a+b\sqrt{-2} \mapsto a-b\sqrt{-2}\;$ (複素共役写像 ${\rm conj}$ )

体と群の関係は次のようになる(この例は単純すぎて中間の体・群がないのであまりありがたみはないけれど)。

体 → 群	群 → 体
$\mathbb{Q}(\sqrt{-2})$ のどの要素も動かさない写像= $\{ {\rm id} \}$	$\{ {\rm id} \}$ のどの写像でも動かないもの= $\mathbb{Q}(\sqrt{-2})$
$\mathbb{Q}$ のどの要素も動かさない写像= $\{ {\rm id}, {\rm conj} \}$	$\{ {\rm id}, {\rm conj} \}$ のどの写像でも動かないもの= $\mathbb{Q}$

例: $\mathbb{Q}\left({}^{ 3}\sqrt{-2},\frac{-1+\sqrt{-3}}{2} \right)$

別の例として $\mathbb{Q}$ に ${}^{ 3}\sqrt{-2}+\frac{-1+\sqrt{-3}}{2} \; (=\alpha+\omega)$ を添付した体 $\mathbb{Q} \left(\alpha+\omega \right)$ を考える。
$\alpha+\omega$ の共役は $\alpha+\omega , \,\alpha+\omega^2 , \,\alpha \omega +\omega , \,\alpha \omega +\omega^2 , \,\alpha \omega^2 +\omega , \,\alpha \omega^2 +\omega^2$ の六つで、自己同型写像も六個あるので、 $\mathbb{Q} \left(\alpha+\omega \right)$ は $\mathbb{Q}$ のガロア拡大になる。 $\alpha+\omega$ を共役に置き換えると $\left( \alpha \omega, \, \alpha \omega^2 , \, \alpha \right)$ の置換を引き起こし、各自己同型写像はこの $\left( \alpha , \, \alpha \omega, \, \alpha \omega^2 \right)$ の置換で表すことができる。
体と自己同型群の間には次のような対応関係がある(置換は $\left(\alpha, \, \alpha \omega, \, \alpha \omega^2 \right)$ の代わりに $\left(1, \, 2, \, 3 \right)$ を使って表す)。

普遍被覆と基本群

被覆のガロア理論と体のガロア理論の間には強い類似関係があるけれど、被覆のガロア理論には体のガロア理論にはない重要な部分がある(というよりもたぶん被覆のガロア理論はその部分が本題なのだけど、文章が長くなってきたのでもう手短にすませたい)。

普遍被覆

世界の形の異なるパラレルワールドが無数にあり、それらの世界の間には被覆という関係があった。そうしたたくさんの世界のなかには他の全ての世界の被覆になっている世界があり、普遍被覆と呼ばれる。
ドラクエ型の世界では、東西南北360度どの方向に進んでも決して反対側から戻ることはなく別の世界が無限に並んでいるという最初に考えた世界が普遍被覆になる。
ガロア被覆でない例としてあげた通路の場合だと、四方向どちらに行ってもそれぞれ別の通路に至り、そこからさらに次の道を選ぶとまたそれぞれ別の通路に至りというようになっていて、来た道をそのまま戻らない限りは常に新しい通路が現れるような世界が普遍被覆になる。
この二つの場合に限らず、違う場所になる可能性があるなら必ず違う場所になるようにして可能な限り世界を広く取ると普遍被覆になる。
普遍被覆の世界にはガロア被覆でない世界にあるような変なループが無い(そもそもループが一つもない)ので、どの共役に跳ぶ場合でも必ずつじつまが合う。したがって普遍被覆はガロア被覆になりガロア対応が成り立つ。普遍被覆は他の全ての世界の被覆になるので、普遍被覆世界の魔法(被覆変換群)を調べれば、全ての被覆関係が判ることになる(変換群の商を取れば各世界での被覆変換群が出てくる)。

基本群

ここでいったん被覆から離れて、そっくりな世界など存在せず各人それぞれ一人だけ存在するという普通の世界を考える。
唐突だけれど空間の繋がり方を調べるのに重要なホモトピー、基本群というものがある。
ホモトピーというのは、まず適当に基点を決めて、そこからゴムひもを好きなように伸ばしていき再び基点に戻ったときにどんなループが作れるかによって空間の形を調べようという考え方。例えば地球のような球面だと、どんなに複雑に歩き回ってもゴムひもを縮めていくとループが一点に収縮してしまう。一方ドラクエのような世界では例えば北に進んで元の位置に戻ってきて作ったループはゴムひもをどのように縮めたり移動させても一点には収縮しない。また何度も一方向に回ってループを作ると回った回数ごとに異なるループになる(ゴムひもをどんな風に変形させても一致しない)。
さまざまなループを考えてそのうちゴムひもを伸び縮みさせて一致するものは同じものとみなし全てのループパターンを集めたものを基本群と呼ぶ。基本群が異なれば空間の繋がり方は異なっている。地球の地表とドラクエ世界の地表は基本群が違うので、繋がり方は異なる(ただし基本群が同じでも空間の繋がり方が同じとは限らない)。
と、このように基本群は世界の形(空間の繋がり方)から決まるもので、被覆とは全く関係なしに説明される。
にもかかわらず基本群と被覆は密接に関係する。
コピーのない普通の世界(底空間)と、普遍被覆の世界の両方を考える。
例えば普通の世界で基点から出発し東に一周回り基点に戻ってきてループを作ったとする。このとき普遍被覆の世界では同じ人物は一つ東の世界にある出発点とは異なる基点(もとの基点の共役点)に到達する。底空間で東に二周してループを作れば、普遍被覆では二つ東の基点に到達する。
逆に普遍被覆の世界で基点から基点の共役点まで歩いていくと、底空間では(基点の共役点が一点しかないので)ループが構成される。

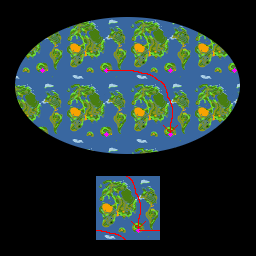
普遍被覆には一点に縮むループしか存在しない。なぜならもしそうでないループが存在したら、そのループになる一帯を別の新たな領域に置き換えればもっと大きな被覆が作れてしまうので(実際には一点に縮むループしか存在しないことが普遍被覆であることの定義になる)。なので普遍被覆側のループは考えなくてもいい。
底空間でひとつループを作ると、普遍被覆側では基点の共役点がひとつ定まる。共役点が定まるとそこへ跳ぶ被覆変換を考えられる。逆に被覆変換をひとつ取り、その魔法で跳ぶ点までゴムひもを持って歩いたと考える。そのとき底空間の側ではループが描かれる。
このように底空間のループ全体(基本群)と普遍被覆での変換全体(被覆変換群)はちょうど一対一に対応して群として同型になる。被覆空間は底空間の外側の話なのに、その被覆空間の関係を教えてくれる被覆変換群のことが底空間の内部の性質である基本群で判るというのが、体のガロア理論にない被覆のガロア理論の特長。

文献

基本群と被覆のガロア理論については、久賀道郎『ガロアの夢』の前半で解説されている。『ガロアの夢』の後半のフックス型微分方程式の話は、ジェレミー・J・グレイ『リーマンからポアンカレにいたる線型微分方程式と群論』が関連することを扱っている。体のガロア理論も基本群のガロア理論も包括するグロタンディークのガロア理論については例えば藤原一宏「ガロア理論」(『現代数学の土壌2』収録)。

ヒルベルトの類体論

さてここで新たに考え方の転換が生まれることになるが、これはクロネッカーによって普及され、デデキントとヴェーバーによって完全に明解な形で浮き彫りにされた。すなわちそれは(数体の整数に関する)数論的考察と(z平面の上に広げられたリーマン面上の代数関数の)関数論的考察との間に一層深い類似関係が成り立つことをしめす。
(クライン『19世紀の数学』p.333)

私はヒルベルトの処へ行ったところが、「お前は代数体の整数論をやるというが、本当にやる積りか?」とえらく懐疑の眼を以って見られた。(……)さて僕が「やる積りです」と言ったところが、「それでは代数函数は何で定まるか?」と早速口頭試問だ。即答ができないでいる裡に、「それはリイマン面で定まる」と先生が自答してしまった。
高木貞治「回顧と展望」

我々は代数函数体の拡大体、とくに不分岐拡大体の理論を被覆Riemann面を用いて考察した。(...)Hilbertが有名なZahlberchtを書き、今日の類体論の雄大な構想を掴んだ頃(1897)、彼がVorbild[手本]として頭に画いていたのが恐らく上述の代数函数体の不分岐Abel拡大体に関する結果であったろう。
(岩澤健吉『代数函数論』緒言)

被覆のガロア理論では、底空間の外側の話である被覆と被覆変換群のことが底空間の内部の話である基本群で理解できた。同様のことが体のガロア理論でも成り立たないか。
とはいっても何の条件もなしでは難しすぎる。
有理数体 $\mathbb{Q}$ のアーベル拡大に関しては、クロネッカー・ヴェーバーの定理によって次のような類似が成り立っている。

被覆	体
底空間	基礎体 $\mathbb{Q}$
普遍被覆	円分体 $\mathbb{Q}(\xi_n)$
普遍被覆は全ての(連結で)不分岐な被覆空間を被覆する	$\mathbb{Q}$ のどのアーベル拡大も円分体の部分体
基本群	既約剰余類群 $(\mathbb{Z}/n\mathbb{Z})^{*}$

しかし円分体で綺麗な性質が成り立つのは1のn乗根 $\xi_n$ があるおかげなのでこれは一般のアーベル拡大には拡張できそうもない(と当時は思われていた)。
ここでヒルベルトは代数的整数論に出てくる不分岐という性質に注目し代数的整数論で重要なイデアル類群を基本群に対応するものとした。

被覆	体
普遍被覆	最大不分岐アーベル拡大(絶対類体)
普遍被覆は全ての(連結で)不分岐な被覆空間を被覆する	どの不分岐アーベル拡大も絶体類体の部分体である
基本群	イデアル類群

ヒルベルトはこの特別な性質を持った体を類体と呼んでさまざまな性質を予想した(今は「絶体類体」とか「ヒルベルト類体」と呼ばれる)。というのがヒルベルトの類体論。ヒルベルトの予想はフルトヴェングラーが証明し、さらに不分岐という条件を取り除き高木貞治の類体論が現れることになる。

浮き輪の上にさまざまな輪っかの絵を描くと、どんな被覆があるかわかってしまう。これがちょうど、代数体の拡大のガロア群のことが基礎体の素数の中に書いてある、と主張する類体論に似ている。ガロア群と基本群は、グロタンディークのスキーム理論によって統合された。
(吉田輝義「類体論と現代数学」)

おとぎ話の魔法の鏡の中に屋外の遠くの景色が映し出されるように、局所体あるいは大域体KのAbel拡大がどれくらいあるか、またそのAbel拡大で何がおきるかという「Kの屋外の景色」が、Kの乗法群あるいはイデール類群という「Kの屋内の鏡」に映しだされてよくわかるようになる、というのが類体論の主な内容である。
(加藤和也、黒川信重、斎藤毅『数論I』)