「コンパクトと点列コンパクト 」で触れたチコノフの定理の証明について。
チコノフの定理は、
おそらくオーソドックスな証明は、「コンパクト」についての
- Xがコンパクト ⇔ Xの閉集合の集まりで有限交差性を持つものは、必ず交差性を持つ。
を使う。
チコノフの定理の間違った証明
まずは、チコノフの定理の間違った証明を示す。(ただし証明の流れは、正しい証明とだいたい同じ)。どこが間違っているかを考えて修正していく。
間違った証明
任意個の位相空間Xλが、それぞれコンパクトとする。直積位相空間Z=ΠXλもコンパクトであることを示す。
Z=ΠXλのXの閉集合の集まりで有限交差性を持つものSを取る。このときSが交差すること(Sの要素の共通集合∩Sが空ではないこと)を示せば、Zがコンパクトであることが示される。
証明の方針は次のようになる:
- Sが交差することを示すには、x∈ ∩S となるxをうまく取ればいい。
- そのxを取るために、Xλのコンパクト性を利用して、xの各座標xλを決める。
座標xλは次のように選ぶ。
- Sが有限交差なら、Sに含まれる各集合をXλに射影した集合 { ρλ(F) | F ∈ S} も有限交差。
- しかしρ(F)は閉集合とは限らないので、閉包をとって Cλ = { cl(ρλ(F)) | F ∈ S} とする。このSλは閉集合族で有限交差。Xλがコンパクトなので交差する。そこでxλ∈ ∩Sλ がとれる。
- 各Xλについて ∩Sλ が空集合ではないので、xλ∈Sλが取れる。(無限個の直積の場合、各λについてxλを取るところで選択公理が必要)。
これでxの各座標xλが決まったので、あとは点xが、Sに含まれるどの閉集合Fにも含まれることを示す。
間違った証明 終わり
上の証明のどこが間違っているか
例1:
例えば、直積空間 X1×X2に対して下の図のように閉集合A、Bを取り、S={A, B} に対して、間違った証明の手順を適用してみる。
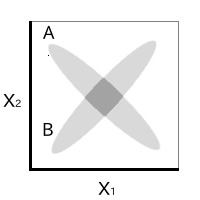
すると x ∈ A∩B であるような点xは、AとBの共通部分である中央の色が濃い部分に含まれるはずなのに、AとBをX1に射影して得られる
ρ1(A)∩ρ2(B)
は、点x∈A∩BのX1座標がとり得る値よりも広い範囲を含んでいる。(X2についても同様)。
つまり、上の証明のように Xλへ射影した集合の要素の交差部分から座標成分 xλ を選ぶと、交差部分にならない座標を選んでしまう可能性がある。
例2:
閉集合がひとつだけの S={A}の場合を考える。
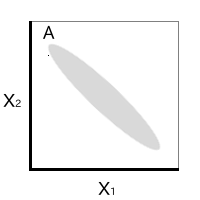
この場合、どの x1 ∈ ρ1(A) を選んでも、共通部分(集合Aそのもの)に含まれる点の座標になり得る。
だけど、同様にx2 ∈ ρ2(A)を選んで、
x = (x1, x2)
としたとき、この点xは集合Aに含まれるとは限らない。(例えば x1は左の方から、x2は下の方から取る)。
- 交差する範囲に含まれていない座標を選ぶかもしれない。
- それぞれの座標は交差する点の座標になっていても、それらの座標を組み合わせた点が交差部分に入っているとは限らない。
という欠陥がある。そのため「点xが、Sに含まれるどの閉集合Fにも含まれることを示す」のところで、実際には示すことができずに証明が破綻する。
欠陥の修正
例えば例1のように「AとBは重なっていないのに、射影ρλ(A)と射影ρλ(B)が重なってしまう場合」については、さらに A∩B を追加してS' ={A, B, A∩B} としてみると、座標の選択範囲が狭くなり交差する部分以外から座標を選ぶ可能性を排除できる。
次に例2の場合。例2のようなことが起こるのは、ふたつの点 p = (p1, p2) と q = (q1, q2)のどちらも交差部分に入っているけど、
x = (x1, x2) = (p1, q2)
は、交差部分に含まれない場合。このような場合、交差部分から点pと点qのうちどちらかを排除する。そのためにはSのどの集合とも有限交差する集合Cを追加して、p ∈ cl(C)、q ∉ cl(C) とする。ここで追加する集合は閉集合である必要はない。
- Xはコンパクト ⇔ Xの部分集合のどんな集まりについても「閉包を取ったものが有限交差性を持つなら、閉包を取ったものは交差性を持つ」
でもあるので、S'に閉集合以外が含まれていてもよい。
それから、実際には交差部分にどんな点が含まれているのかはよく分からないのだから、そのような集合Cを具体的に与えることはできない。でも、与えられた集合族Sに対して、有限交差性を満たすようにしながらどんどん集合を追加して、これ以上もう追加できない状態(有限交差性についての極大集合) S' にしておけば、上のような問題を引き起こす点p、qは存在しなくなる。(もしそういう2点p、qが存在したら、さらに C={p} を追加すると、有限交差性を満たしながら点qを交差部分から排除できる。(位相によっては、{p}は閉集合とは限らないことに注意)。しかしS'はもうそれ以上集合を追加できない状態なので、すでにそのような点の組p、qは排除されている)。
例1の場合についても、Sに対して極大な集合族S' ⊇ S を取れば、A、B ∈S' なら A∩B ∈S' となる。
つまり、有限交差性を持つ集合族Sを直接扱うのではなく、それを含む極大な集合族S'を取っておけば、間違った証明での欠陥が生じない。
チコノフの定理の正しい証明の流れ
上で分かった修正を取り入れると、証明の流れは次のようになる。
- Z=ΠXλの閉集合の集まりで有限交差性を持つ集合族Sがあったとする。
- Sを含み有限交差性を持つ集合族で極大なもの S'⊇S を取る。(そのようなS'が存在することは、ツォルンの補題によって保証される)。
- S'も有限交差性を満たすので、閉包をとった{cl(A) | A∈S'}は交差する部分を持つはず。交差する部分に含まれる点 x ∈ ∩cl(A) (A∈S')があることを示す。
- S'に含まれる各集合をXλに射影した集合族S'λを考える。このS'λは有限交差性を満たし、Xλはコンパクトなので、∩cl(A) (A∈S'λ) は空集合ではない。
- 各Xλについて座標 xλ ∈ ∩cl(A) (A∈S'λ) を選んで、点x = (xλ) を取る。(ここで選択公理が使われる)。
- どのA∈S'についても、x∈cl(A) となることが示せる。
- 直積位相の定義(開集合の基(base)の取り方)は、この部分で使われる。「 x∈cl(A) 」というのは、「 ΠXλの開集合の基Bで点xを含むものは必ずAと交わる、つまりB∩A≠φとなる 」ということなので。
- S⊆S' なので、どのA∈Sについても、x∈A となる。(Sの要素は閉集合なのでcl(A)=A)。つまりSは交差性を持つ。
- 1→7によって「Sが有限交差なら交差」が示せたので、Zはコンパクト。
極大な集合族を取る部分以外は、間違った証明と同じ流れ。
フィルターを用いた証明 1
フィルターによるコンパクト性の特徴づけ(の一つ)は
- Xはコンパクト ⇔ Xのフィルターは触点を必ず持つ。
というものだった。これは、
- Xはコンパクト ⇔ Xの閉集合の集まりで有限交差性を持つものは、必ず交差性を持つ。
- Xはコンパクト ⇔ Xの部分集合のどんな集まりについても「閉包を取ったものが有限交差性を持つなら、閉包を取ったものは交差性を持つ」
とよく似ていた。(フィルターは定義から常に有限交差性を持ち、「フィルターが触点を持つ」は「フィルターの各要素の閉包は、交差性を持つ」と同じことなので)。
そのため、上の証明の初めの部分の
- Z=ΠXλの閉集合の集まりで有限交差性を持つ集合族Sがあったとする。
- Sを含み有限交差性を持つ集合族で極大なもの S'⊇S を取る。
を
- Z=ΠXλのフィルターSがあったとする。
- Sを含み有限交差性を持つ集合族で極大なもの S'⊇S を取る。(※このS'もフィルターになる。極大フィルター)。
に置き換えれば、ほとんど同じようにしてチコノフの証明することができる。
フィルターを用いた証明 2
上で見たように、チコノフの定理を証明するには、有限交差性な集合(閉集合の集まりだったりフィルターだったり)に対して、その極大な集合を取る操作が必要だった。
しかし、コンパクト性の特徴付け(あるいは定義)として、
- Xはコンパクト ⇔ Xの極大フィルターは必ず収束する。
を使うと話が変わる。
この特徴付けでは、初めから極大なものである「極大フィルター」を使っているので、改めて極大なものを取る操作をする必要がない。そのため証明の流れが少なくとも見かけ上は簡単になる。次のような感じになる。
- 各Xλはコンパクトで、Z=ΠXλ とする。Zがコンパクトだと示したい。
- Z上の極大フィルターFを取る。
- フィルターの各要素をXλに射影した集合Fλを考える。すると、このFλはXλ上の極大フィルターになる(ことを示す)。よってFλは収束するので、収束点xλを取る。
- 各成分がxλであるx∈Zを取ると、フィルターFはxに収束する(ことを、直積位相の定義から示す)。
- 極大フィルターFが必ず収束するので、Zはコンパクト。証明終り
チコノフの定義の証明は簡潔になるけど、フィルターの導入コストもあるから、この証明が一概に良いと言えるのかどうかは分からない。